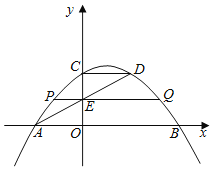
【題目】如圖，拋物線
與x軸相交于
兩點，與
軸相交于點
，點
在拋物線上，且
．
與軸相交于點
，過點的直線
平行于
軸，與拋物線相交于
兩點，則線段的長為_____．
【答案】
【解析】
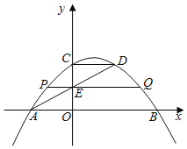
利用二次函數(shù)圖象上點的坐標(biāo)特征可求出點A，B，C，D的坐標(biāo)，由點A，D的坐標(biāo)，利用待定系數(shù)法可求出直線AD的解析式，利用一次函數(shù)圖象上點的坐標(biāo)特征可求出點E的坐標(biāo)，再利用二次函數(shù)圖象上點的坐標(biāo)特征可得出點P，Q的坐標(biāo)，進(jìn)而可求出線段PQ的長．
解：由圖可知，
當(dāng)
時，
，
解得：
，
，
∴點
的坐標(biāo)為
；
當(dāng)
時，
，
∴點
的坐標(biāo)為(0，2)；
當(dāng)
時，
，
解得：
，
，
∴點
的坐標(biāo)為
．
設(shè)直線
的解析式為
，
將
，
代入
，得：
，解得：
，
∴直線的解析式為
．
當(dāng)時，
，
∴點
的坐標(biāo)為
．
當(dāng)
時，
，
解得：
，
，
∴點
的坐標(biāo)為
，點
的坐標(biāo)為
，
∴
．
故答案為：．
口算小狀元口算速算天天練系列答案科目：初中數(shù)學(xué) 來源： 題型：
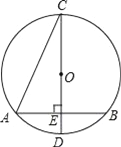
【題目】如圖，已知⊙O的直徑CD垂直于弦AB，垂足為點E，∠ACD=22.5°，若CD=6cm，則AB的長為（ ）
A. 4cm B. 3
cm C. 2
cm D. 2
cm
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
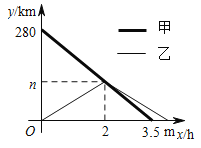
【題目】甲、乙兩車分別從
兩地同時出發(fā)，沿同一條公路相向行駛，相遇后，甲車?yán)^續(xù)以原速行駛到
地，乙車立即以原速原路返回到地，甲、乙兩車距地的路程
與各自行駛的時間
之間的關(guān)系如圖所示．
⑴
________，
________；
⑵求乙車距地的路程
關(guān)于
的函數(shù)解析式，并寫出自變量的取值范圍；
⑶當(dāng)甲車到達(dá)地時，求乙車距地的路程
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，正方形ABCD的頂點A、D分別在x軸、y軸的正半軸上，若反比例函數(shù)y=
（x＞0）的圖象經(jīng)過另外兩個頂點B、C，且點B（6，n），（0＜n＜6），則k的值為（ ）
A. 18B. 12C. 6D. 2
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖1，在△ABC中，BA=BC，點D，E分別在邊BC、AC上，連接DE，且DE=DC．
（1）問題發(fā)現(xiàn)：若∠ACB=∠ECD=45°，則
．
（2）拓展探究，若∠ACB=∠ECD=30°，將△EDC繞點C按逆時針方向旋轉(zhuǎn)α度（0°＜α＜180°），圖2是旋轉(zhuǎn)過程中的某一位置，在此過程中
的大小有無變化？如果不變，請求出的值，如果變化，請說明理由．
（3）問題解決：若∠ACB=∠ECD=β（0°＜β＜90°），將△EDC旋轉(zhuǎn)到如圖3所示的位置時，則的值為 ．（用含β的式子表示）
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖1，四邊形
內(nèi)接于圓
，
是圓的直徑，過點
的切線與
的延長線相交于點
．且
（1）求證：
；
（2）過圖1中的點
作
，垂足為
（如圖2），當(dāng)
，
時，求圓的半徑．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
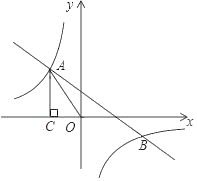
【題目】如圖，一次函數(shù)
的圖象與反比例函數(shù)
的圖象交于第二、四象限內(nèi)的點
和點
．過點
作
軸的垂線，垂足為點
，
的面積為4．
（1）分別求出
和
的值；
（2）結(jié)合圖象直接寫出
的解集；
（3）在軸上取點
，使
取得最大值時，求出點的坐標(biāo)．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
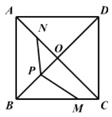
【題目】如圖，在正方形ABCD中，AB=8，AC與BD交于點O，N是AO的中點，點M在BC邊上，且BM=6. P為對角線BD上一點，則PM—PN的最大值為___.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
