我市某游樂場投資150萬元引進一項大型游樂設施.若不計維修保養費用,預計開放后每月可創收35萬元.而該游樂設施開放后,從第1個月到第x個月的維修保養費用累計為y(萬元),且y=ax2+bx;若將創收扣除投資和維修保養費用稱為游樂場的純收益g(萬元),g也是關于x的解析式;
(1)若維修保養費用第1個月為2萬元,第2個月累計為6萬元.求y關于x的解析式;
(2)求純收益g關于x的解析式;
(3)問設施開放幾個月后,游樂場的純收益達到最大?并求出該游樂場的最大純收益.
【答案】
分析:(1)將x與y的值代入y=ax
2+bx建立二元一次方程組求出其解即可;
(2)純收益g=x個月的總利潤-總投資150萬-x個月的維修保養費用,化簡即可求的g關于x的解析式;
(3)先用配方法把解析式化為頂點式,求得頂點坐標即可知其最大值問題;只有當g>0時,才能回收投資,所以可根據二次函數g>0時對應的x值來確定其在第6個月可回收投資.
解答:解:(1)由題意得:x=1時y=2;
x=2時,y=6代入得:
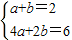
解之得:
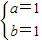
.
∴y=x
2+x;
(2)由題意得:
g=35x-150-(x
2+x)
g=-x
2+34x-150;
(3)∵g=-x
2+34x-150;
∴g=-x
2+34x-150=-(x-17)
2+139,
∴a=-1<0,拋物線開口向下,g有最大值.
∴當x=17時,g最大值=139,
點評:本題考查了用待定系數法求二次函數解析式及二次函數的實際應用.此題為數學建模題,借助二次函數解決實際問題.

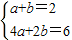
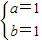 .
.

 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案