【題目】如圖，
的面積為
，
、
分別是
，
上的點，且
,
．連接
,
交于點
,連接
并延長交
于點
．則四邊形
的面積為_____．
【答案】
.
【解析】
先畫出圖形,再作DJ∥EC交AB于J,交AH于K,作DG∥BC交AH于G.由題推出EF:FC=1:3,BH:CH=1:2,求出△BEF,△BFH的面積即可.
根據題意畫出圖形:
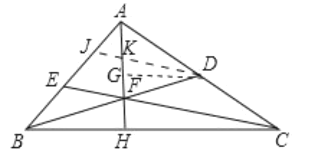
作DJ∥EC交AB于J,交AH于K作DG∥BC交AH于G.
∵DJ∥EC,AD=DC,
∴AJ=JE,AK=KF,
∴EF=2JK,DJ=2EF,CF=2DK,
設JK=m,則EF=2m,DJ=4m,DK=3m,CF=6m,
∴EF:CF=1:3,
∵AE= 2BE,
∴BE=EJ,
∵EF∥DJ,
∴BF=DF,
∵GD∥BH,
∴∠GDF=∠FBH,
∵∠GFD=∠HFB,BF=DF,
∴△DFG≌△BFH（ASA）,
∴DG=BH,
∵DG∥CH,AD=DC,
∴AG=GH,
∴CH=2DG,
∴BH=2CH,
∵BE=
AB,
∴S△BEC=S△ABC=
,
∵EG=
EC,
∴S△BEF=S△BEC=
,S△BFC=
,
∵BH=BC,
∴S△BHF=×=,
∴S四邊形BEFH=+=
閱讀快車系列答案科目：初中數學 來源： 題型：
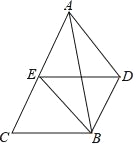
【題目】如圖，已知DB∥AC，E是AC的中點，DB＝AE，連結AD、BE．
（1）求證：四邊形DBCE是平行四邊形；
（2）若要使四邊形ADBE是矩形，則△ABC應滿足什么條件？說明你的理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將邊長為
的正方形的邊長增加
，得到一個邊長為
的正方形.在圖1的基礎上，某同學設計了一個解釋驗證
的方案（詳見方案1）
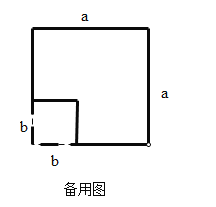
方案1.如圖2，用兩種不同的方式表示邊長為的正方形的面積.
方式1：
方式2：
因此，
（1）請模仿方案1，在圖1的基礎上再設計一種方案，用以解釋驗證；
（2）如圖3，在邊長為的正方形紙片上剪掉邊長為的正方形，請在此基礎上再設計一個方案用以解釋驗證
.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某單位欲從內部招聘管理人員一名，對甲、乙、丙三名候選人進行了筆試和面試兩項測試，三人的測試成績如下表所示：
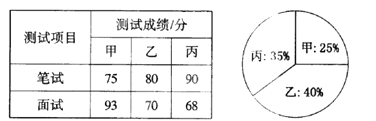
根據錄用程序，組織200名職工對三人利用投票推薦的方式進行民主評議，三人得票率（沒有棄權票，每位職工只能推薦1人）如上圖所示，每得一票記作1分．
（l）請算出三人的民主評議得分；
（2）如果根據三項測試的平均成績確定錄用人選，那么誰將被錄用（精確到 0.01 )?
（3）根據實際需要，單位將筆試、面試、民主評議三項測試得分按 4 : 3 : 3 的比例確定個人成績，那么誰將被錄用？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】拋物線y=ax2+bx+3（a≠0）經過點A（﹣1，0），B（
，0），且與y軸相交于點C．
（1）求這條拋物線的表達式；
（2）求∠ACB的度數；
（3）設點D是所求拋物線第一象限上一點，且在對稱軸的右側，點E在線段AC上，且DE⊥AC，當△DCE與△AOC相似時，求點D的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
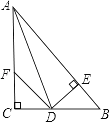
【題目】如圖：在△ABC中，∠C=90°，AD是∠BAC的平分線，DE⊥AB于E，F在AC上，BD=DF；
求證：（1）CF=EB．
（2）AB=AF+2EB．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知AB是⊙O的直徑，弦CD⊥AB于H，過CD延長線上一點E作⊙O的切線交AB的延長線于F，切點為G，連接AG交CD于K．
（1）如圖1，求證：KE=GE；
（2）如圖2，連接CABG，若∠FGB=
∠ACH，求證：CA∥FE；
（3）如圖3，在（2）的條件下，連接CG交AB于點N，若sinE=
，AK=
，求CN的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
