
已知a、b可以取﹣2、﹣1、1、2中任意一個值(a≠b),則直線y=ax+b的圖象不經過第四象限的概率是 .
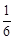
【解析】
試題分析:根據概率的求法,找準兩點:①全部等可能情況的總數;②符合條件的情況數目;二者的比值就是其發生的概率。因此,列表或畫樹狀圖得出所有等可能的結果數,找出a與b都為正數,即為直線y=ax+b不經過第四象限的情況數,即可求出所求的概率:
列表如下:
|
|
﹣2 |
﹣1 |
1 |
2 |
|
﹣2 |
|
(﹣1,﹣2) |
(1,﹣2) |
(2,﹣2) |
|
﹣1 |
(﹣2,﹣1) |
|
(1,﹣1) |
(2,﹣1) |
|
1 |
(﹣2,1) |
(﹣1,1) |
|
(2,1) |
|
2 |
(﹣2,2) |
(﹣1,2) |
(1,2) |
|
∵所有等可能的情況數有12種,其中直線y=ax+b不經過第四象限情況數有2種,
∴直線y=ax+b的圖象不經過第四象限的概率是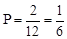 。
。


科目:初中數學 來源:2013年湖南省株洲市中考數學試卷(解析版) 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com