
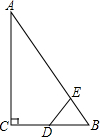
 如圖,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,點D為BC的中點,動點E從點A出發(fā),沿著A→B→A的方向以1cm/s的速度運動,當回到點A時停止運動,連接DE.設點E的運動時間為t(s),△BDE的面積為S(cm2)(這里規(guī)定:線段是面積為0的幾何圖形).
如圖,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,點D為BC的中點,動點E從點A出發(fā),沿著A→B→A的方向以1cm/s的速度運動,當回到點A時停止運動,連接DE.設點E的運動時間為t(s),△BDE的面積為S(cm2)(這里規(guī)定:線段是面積為0的幾何圖形).分析 (1)根據(jù)已知和余弦的概念求出AB的長;
(2)作DF⊥AB于點F,根據(jù)三角函數(shù)的概念求出DF的長,分當0≤t≤4時和當4≤t≤8時兩種情況表示出S與t之間的函數(shù)關系式;
(3)分∠EDB=90°和∠DEB=90°兩種情況結合銳角三角函數(shù)的概念進行解答即可.
解答 解:(1)在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴cosB=$\frac{BC}{AB}$=$\frac{1}{2}$,
∴AB=4cm;
(2)過點D作DF⊥AB于點F,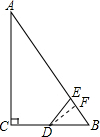
在Rt△BDF中,∠DBF=60°,
∴sinB=$\frac{DF}{BD}$,
∴DF=$\frac{\sqrt{3}}{2}$,
①當0≤t≤4時,S=$\frac{1}{2}$•BE•DF=$\frac{1}{2}$(4-t)×$\frac{\sqrt{3}}{2}$=-$\frac{\sqrt{3}}{4}$t+$\sqrt{3}$,
②當4≤t≤8時,S=$\frac{1}{2}$•BE•DF=$\frac{1}{2}$(t-4)×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$t-$\sqrt{3}$;
(3)當∠EDB=90°,cosB=$\frac{BD}{BE}$=$\frac{1}{2}$,
∴$\frac{1}{4-t}$=$\frac{1}{2}$或$\frac{1}{t-4}$=$\frac{1}{2}$,
解得t=2或t=6,
當∠DEB=90°,cosB=$\frac{BE}{BD}$=$\frac{1}{2}$,
∴4-t=$\frac{1}{2}$或t-4=$\frac{1}{2}$,
解得t=3.5或t=4.5.
當t=2、t=6、t=3.5、t=4.5時,△BDE是直角三角形.
點評 本題考查的是銳角三角函數(shù)、一次函數(shù)的應用和直角三角形的知識,掌握銳角三角函數(shù)的概念、正確進行分情況討論是解題的關鍵.


科目:初中數(shù)學 來源: 題型:解答題
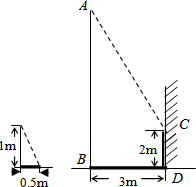 如圖,某一時刻,小明垂直地面豎起一根1m高的直桿,量得其在陽光下的影長為0.5m,此時,旁邊一電線桿AB在陽光下的影子分別落在了地上和墻上,他又量得電線桿AB落在地面上的影子部分BD長為3m,落在墻上的影子部分CD高為2m,小明用這些數(shù)據(jù)很快算出了電線桿AB的高,請你計算一下:
如圖,某一時刻,小明垂直地面豎起一根1m高的直桿,量得其在陽光下的影長為0.5m,此時,旁邊一電線桿AB在陽光下的影子分別落在了地上和墻上,他又量得電線桿AB落在地面上的影子部分BD長為3m,落在墻上的影子部分CD高為2m,小明用這些數(shù)據(jù)很快算出了電線桿AB的高,請你計算一下:查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | xy | B. | y | C. | x | D. | x$\sqrt{y}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | $1{\frac{1}{2}^{\;}}$x | B. | x÷y | C. | m×2 | D. | 3mn |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
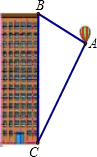 如圖,熱氣球的探測器顯示,從熱氣球看一棟高樓頂部的仰角為35.6°,看這棟高樓底部的俯角的正切值為2,熱氣球與高樓的水平距離為90米,這棟高樓有多高(結果精確到0.1米.參考數(shù)據(jù):sin35.6°=0.582,cos35.6°=0.813,tan35.6°=0.716)?
如圖,熱氣球的探測器顯示,從熱氣球看一棟高樓頂部的仰角為35.6°,看這棟高樓底部的俯角的正切值為2,熱氣球與高樓的水平距離為90米,這棟高樓有多高(結果精確到0.1米.參考數(shù)據(jù):sin35.6°=0.582,cos35.6°=0.813,tan35.6°=0.716)?查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com