
【題目】圖1是用繩索織成的一片網的一部分,小明探索這片網的結點數(V),網眼數(F),邊數(E)之間的關系,他采用由特殊到一般的方法進行探索,列表如下:
特殊網圖 |
|
|
|
|
結點數(V) | 4 | 6 | 9 | 12 |
網眼數(F) | 1 | 2 | 4 | 6 |
邊數(E) | 4 | 7 | 12 | ☆ |
表中“☆”處應填的數字為_____;根據上述探索過程,可以猜想V,F,E之間滿足的等量關系為_____;
如圖2,若網眼形狀為六邊形,則V,F,E之間滿足的等量關系為___ .

【答案】17 V+F﹣E=1 V+F﹣E=1.
【解析】
根據表中數據可知,邊數E比結點數V與網眼數F的和小1,從而得到6個網眼時的邊數;依據以上規律可得V+F-E=1;類比網眼為四邊形時的方法,可先羅列網眼數是1、2、3時的V、F、E,從而得出三者間關系.
由表格數據可知,1個網眼時:4+1-4=1;
2個網眼時:6+2-7=1;
3個網眼時:9+4-12=1;
4個網眼時:12+6-☆=1,故“☆”處應填的數字為17;
據此可知,V+F-E=1;
若網眼形狀為六邊形時,
一個網眼時:V=6,F=1,E=6,此時V+F-E=6+1-6=1;
二個網眼時:V=10,F=2,E=11,此時V+F-E=10+2-11=1;
三個網眼時:V=13,F=3,E=15,此時V+F-E=13+3-15=1;
故若網眼形狀為六邊形時,V,F,E之間滿足的等量關系為:V+F-E=1.
故答案為:17,V+F-E=1,V+F-E=1.


科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠B=90°,BC=2AB=8,點D,E分別是邊BC,AC的中點,連接DE.將△EDC繞點C按順時針方向旋轉,當△EDC旋轉到A,D,E三點共線時,線段BD的長為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們把兩條中線互相垂直的三角形稱為“中垂三角形”,例如圖1,圖2,圖3中,AF,BE是△ABC的中線,AF⊥BE,垂足為P,像△ABC這樣的三角形均為“中垂三角形”,設BC=a,AC=b,AB=c.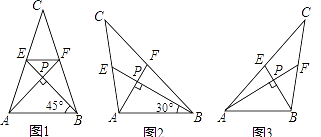
(1)【特例探索】
如圖1,當∠ABE=45°,c=2 ![]() 時,a= , b=;如圖2,當∠ABE=30°,c=4時,a= , b=;
時,a= , b=;如圖2,當∠ABE=30°,c=4時,a= , b=;
(2)【歸納證明】
請你觀察(1)中的計算結果,猜想a2 , b2 , c2三者之間的關系,用等式表示出來,請利用圖3證明你發現的關系式;
(3)【拓展應用】
如圖4,在ABCD中,點E,F,G分別是AD,BC,CD的中點,BE⊥EG,AD=2 ![]() ,AB=3.求AF的長.
,AB=3.求AF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
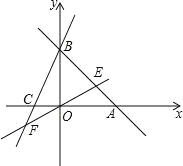
【題目】直線AB:y=﹣x+b分別與x,y軸交于A(6,0)、B 兩點,過點B的直線交x軸負半軸于C,且OB:OC=3:1.
(1)求點B的坐標.
(2)求直線BC的解析式.
(3)直線 EF 的解析式為y=x,直線EF交AB于點E,交BC于點 F,求證:S△EBO=S△FBO.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】水是人類的生命之源.為了鼓勵居民節約用水,相關部門實行居民生活用水階梯式計量水價政策.若居民每戶每月用水量不超過10立方米,每立方米按現行居民生活用水水價收費(現行居民生活用水水價=基本水價+污水處理費);若每戶每月用水量超過10立方米,則超過部分每立方米在基本水價基礎上加價100%,每立方米污水處理費不變.甲用戶4月份用水8立方米,繳水費27.6元;乙用戶4月份用水12立方米,繳水費46.3元.(注:污水處理的立方數=實際生活用水的立方數)
(1)求每立方米的基本水價和每立方米的污水處理費各是多少元?
(2)如果某用戶7月份生活用水水費計劃不超過64元,該用戶7月份最多可用水多少立方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小南身高為163cm,一張紙的厚度為0.09mm,現將這張紙連續對折(假設對折始終能成功),若連續對折![]() 次后,紙的厚度超過了小南的身高,那么
次后,紙的厚度超過了小南的身高,那么![]() 的值最小是
的值最小是
A. 12 B. 13 C. 14 D. 15
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線 ![]() 與x軸的負半軸交于點A,與y軸交于點B,連結AB.點C
與x軸的負半軸交于點A,與y軸交于點B,連結AB.點C ![]() 在拋物線上,直線AC與y軸交于點D.
在拋物線上,直線AC與y軸交于點D.
(1)求c的值及直線AC的函數表達式;
(2)點P在x軸的正半軸上,點Q在y軸正半軸上,連結PQ與直線AC交于點M,連結MO并延長交AB于點N,若M為PQ的中點.
①求證:△APM∽△AON;
②設點M的橫坐標為m , 求AN的長(用含m的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數 ![]() 的圖像與
的圖像與 ![]() 軸交于
軸交于 ![]() 、
、 ![]() 兩點,與
兩點,與 ![]() 軸交于點
軸交于點 ![]() ,
, ![]() .點
.點 ![]() 在函數圖像上,
在函數圖像上, ![]() 軸,且
軸,且 ![]() ,直線
,直線 ![]() 是拋物線的對稱軸,
是拋物線的對稱軸, ![]() 是拋物線的頂點.
是拋物線的頂點.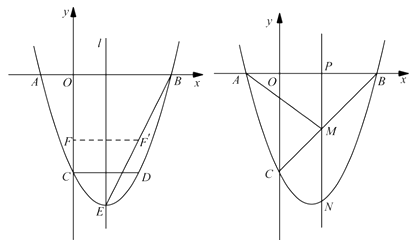
圖 ① 圖②
(1)求 ![]() 、
、 ![]() 的值;
的值;
(2)如圖①,連接 ![]() ,線段
,線段 ![]() 上的點
上的點 ![]() 關于直線
關于直線 ![]() 的對稱點
的對稱點 ![]() 恰好在線段
恰好在線段 ![]() 上,求點
上,求點 ![]() 的坐標;
的坐標;
(3)如圖②,動點 ![]() 在線段
在線段 ![]() 上,過點
上,過點 ![]() 作
作 ![]() 軸的垂線分別與
軸的垂線分別與 ![]() 交于點
交于點 ![]() ,與拋物線交于點
,與拋物線交于點 ![]() .試問:拋物線上是否存在點
.試問:拋物線上是否存在點 ![]() ,使得
,使得 ![]() 與
與 ![]() 的面積相等,且線段
的面積相等,且線段 ![]() 的長度最小?如果存在,求出點
的長度最小?如果存在,求出點 ![]() 的坐標;如果不存在,說明理由.
的坐標;如果不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電信公司推出一款移動話費套餐,資費標準見下表:
套餐月費/元 | 套餐內容 | 套餐外資費 | |
主叫限定時間/分鐘 | 被叫 | 主叫超時費 (元/分鐘) | |
58 | 50 | 免費 | 0.25 |
88 | 150 | 0.20 | |
118 | 350 | 0.15 | |
說明:①主叫:主動打電話給別人;被叫:接聽別人打進來的電話. ②若辦理的是月使用費為 58 元的套餐,主叫時間不超過 50 分鐘時,當月話費即 為 58 元;主叫時間為 60 分鐘,則當月話費為 58+0.25×(60-50)=60.5 元. | |||
小文辦理的是月使用費為 88 元的套餐,亮亮辦理的是月使用費為 118 元的套餐.
(1)小文當月的主叫時間為 220 分鐘,則該月她的話費需多少元?
(2)某月小文和亮亮的主叫時間都為 m 分鐘 (m 350) ,請用含 m 的代數式表示該月他們的 話費差.
(3)某月小文和亮亮的話費相同,但主叫時間比亮亮少 100 分鐘,求小文和亮亮的主叫時間 分別為多少分鐘?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com