
【題目】直線AB:y=﹣x+b分別與x,y軸交于A(6,0)、B 兩點,過點B的直線交x軸負半軸于C,且OB:OC=3:1.
(1)求點B的坐標.
(2)求直線BC的解析式.
(3)直線 EF 的解析式為y=x,直線EF交AB于點E,交BC于點 F,求證:S△EBO=S△FBO.
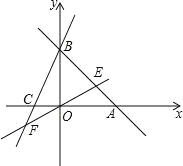
【答案】(1) B (0,6);(2) y=3x+6;(3)見解析.
【解析】
(1)先把A點坐標代入y=-x+b求出b=6,得到直線AB的解析式為y=-x+6,然后求自變量為0時的函數值即可得到點B的坐標;
(2)利用OB:OC=3:1得到OC=2,C點坐標為(-2,0),然后利用待定系數法求直線BC的解析式;
(3)根據兩直線相交的問題,通過解方程組![]() 得E(3,3),解方程組
得E(3,3),解方程組![]() 得F(-3,-3),然后根據三角形面積公式可計算出S△EBO=9,S△FBO=9,S△EBO=S△FBO.
得F(-3,-3),然后根據三角形面積公式可計算出S△EBO=9,S△FBO=9,S△EBO=S△FBO.
(1)把A(6,0)代入y=-x+b得-6+b=0,解得b=6,
所以直線AB的解析式為y=-x+6,
當x=0時,y=-x+6=6,
所以點B的坐標為(0,6);
(2)解:∵OB:OC=3:1,而OB=6,
∴OC=2,
∴C點坐標為(-2,0),
設直線BC:y=mx+n,
把B(0,6),C(-2,0)分別代入得![]() ,解得
,解得![]() ,
,
∴直線BC的解析式為y=3x+6;
(3)證明:解方程組![]() 得
得![]() ,則E(3,3),
,則E(3,3),
解方程組![]() 得
得![]() ,則F(-3,-3),
,則F(-3,-3),
所以S△EBO=![]() ×6×3=9,
×6×3=9,
S△FBO=![]() ×6×3=9,
×6×3=9,
所以S△EBO=S△FBO.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】“智慧南京、綠色出行”,騎共享單車出行已經成為一種時尚.記者隨機調查了一些騎共享單車的秦淮區市民,并將他們對各種品牌單車的選擇情況繪制成圖①和圖②的統計圖(A:摩拜單車;B:ofo單車;C:HelloBike).請根據圖中提供的信息,解答下列問題: 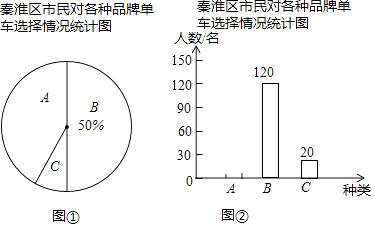
(1)在圖①中,C部分所占扇形的圓心角度數為°;
(2)將圖②補充完整;
(3)根據抽樣調查結果,請你估計某天該區48萬名騎共享單車的市民中有多少名選擇摩拜單車?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2E3E4B3…按如圖所示的方式放置,其中點B1在y軸上,點C1、E1、E2、C2、E3、E4、C3…在x軸上,已知正方形A1B1C1D1的邊長為l,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,則正方形A2017B2017C2017 D2017的邊長是( ) 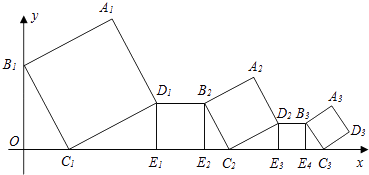
A.( ![]() )2016
)2016
B.( ![]() )2017
)2017
C.( ![]() )2016
)2016
D.( ![]() )2017
)2017
查看答案和解析>>
科目:初中數學 來源: 題型:
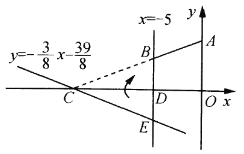
【題目】如圖,在平面直角坐標系![]() 中,
中,![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 與
與![]() 軸及直線
軸及直線![]() 分別交于點
分別交于點![]() .點
.點![]() 關于
關于![]() 軸對稱,連接
軸對稱,連接![]() .
.
(1)求點![]() 的坐標及直線
的坐標及直線![]() 的表達式;
的表達式;
(2)設面積的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 時,嘉琪有個想法:“將
時,嘉琪有個想法:“將![]() 沿
沿![]() 軸翻折到
軸翻折到![]() 的位置,
的位置,![]() 與四邊形
與四邊形![]() 拼接后可看成
拼接后可看成![]() ,這樣求
,這樣求![]() 便轉化為直接求
便轉化為直接求![]() 的面積不更快捷嗎?”但大家經反復驗算,發現
的面積不更快捷嗎?”但大家經反復驗算,發現![]() ,請通過計算解釋他的想法錯在哪里.
,請通過計算解釋他的想法錯在哪里.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】班長調查了三班近 10 天的數學課堂小測驗,在這 10 天,小測驗的不及格人數為(單位:個)0,2,0, 3,1,1,0,2,5,1.在這 10 天中小測驗不及格的人數( )
A. 中位數為 1.5 B. 方差為 1.5 C. 極差為 1.5 D. 標準差為 1.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】八年級(1)班研究性學習小組為研究全校同學課外閱讀情況,在全校隨機邀請了部分同學參與問卷調查,統計同學們一個月閱讀課外書的數量,并繪制了以下統計圖.

請根據圖中信息解決下列問題:
(1)共有多少名同學參與問卷調查;
(2)補全條形統計圖和扇形統計圖;
(3)全校共有學生1500人,請估計該校學生一個月閱讀2本課外書的人數約為多少.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1是用繩索織成的一片網的一部分,小明探索這片網的結點數(V),網眼數(F),邊數(E)之間的關系,他采用由特殊到一般的方法進行探索,列表如下:
特殊網圖 |
|
|
|
|
結點數(V) | 4 | 6 | 9 | 12 |
網眼數(F) | 1 | 2 | 4 | 6 |
邊數(E) | 4 | 7 | 12 | ☆ |
表中“☆”處應填的數字為_____;根據上述探索過程,可以猜想V,F,E之間滿足的等量關系為_____;
如圖2,若網眼形狀為六邊形,則V,F,E之間滿足的等量關系為___ .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 的中點.過點
的中點.過點 ![]() 作
作 ![]() ,垂足為
,垂足為 ![]() .將
.將 ![]() 沿點
沿點 ![]() 到點
到點 ![]() 的方向平移,得到
的方向平移,得到 ![]() .設
.設 ![]() 、
、 ![]() 分別是
分別是 ![]() 、
、 ![]() 的中點,當點
的中點,當點 ![]() 與點
與點 ![]() 重合時,四邊形
重合時,四邊形 ![]() 的面積為( )
的面積為( )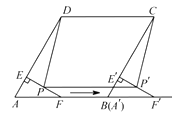
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)先化簡,再求值: 2(m2 mn 1) 3(![]() m2 2mn 4) ,其中 m
m2 2mn 4) ,其中 m ![]() ,n 3 .
,n 3 .
(2)已知 2a b 5 0 ,求整式 6a b 與 2a 3b 27 的和的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com