
 如圖,在矩形ABCD中,AB=2,∠ADB=30°,沿對角線BD折疊,使△ABD和△EBD落在同一平面內,則A,E之間的距離為2.
如圖,在矩形ABCD中,AB=2,∠ADB=30°,沿對角線BD折疊,使△ABD和△EBD落在同一平面內,則A,E之間的距離為2. 分析 由矩形的性質,折疊的性質可證△ABD≌△EDB,根據全等三角形對應邊上的高相等,可證四邊形ABDE為梯形,再根據角的關系證明△ABE為等腰三角形即可.
解答 解:由矩形的性質可知△ABD≌△CDB,由折疊的性質可知△CDB≌△EDB,則△ABD≌△EDB,
根據全等三角形對應邊上的高相等,可知AE∥BD,
∵AD∥BC,△CDB≌△EDB,
∴∠EBD=∠CBD=∠ADB=30°,
∴∠ABE=90°-∠EBD-∠CBD=30°,
∠AEB=∠EBD=30°,即∠ABE=∠AEB,
∴AE=AB=2,
故答案為2.
點評 本題考查了圖形的翻折變換,解題過程中應注意折疊是一種對稱變換,它屬于軸對稱,根據軸對稱的性質,折疊前后圖形的形狀和大小不變,如本題中折疊前后對應線段、角相等.


科目:初中數學 來源: 題型:選擇題
| 日期 | 1號 | 2號 | 3號 | 4號 | 5號 | 6號 | 7號 |
| 空氣質量指數 | 446 | 402 | 456 | 499 | 500 | 434 | 105 |
| A. | 446,416 | B. | 446,406 | C. | 451,406 | D. | 499,416 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 銷售單價x(元) | 12 | 14 | 16 | 18 |
| 年銷售量y(萬件) | 7 | 6 | 5 | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
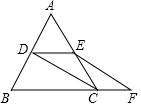 如圖,△ABC是等邊三角形,點D,E分別為AB、AC的中點,延長BC至點F,使CF=$\frac{1}{2}$BC,連接CD和EF,求證:四邊形DEFC是平行四邊形.
如圖,△ABC是等邊三角形,點D,E分別為AB、AC的中點,延長BC至點F,使CF=$\frac{1}{2}$BC,連接CD和EF,求證:四邊形DEFC是平行四邊形.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com