
如圖,二次函數y= ?x2axb的圖象與x軸交于A(?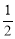 ,0)、B(2,0)兩點,且與y軸交于點C.
,0)、B(2,0)兩點,且與y軸交于點C.
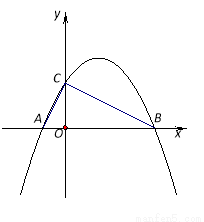
(1)求該拋物線的解析式,并判斷△ABC的形狀;
(2)在x軸上方的拋物線上有一點D,且以A、C、D、B四點為頂點的四邊形是等腰梯形,請直接寫出D點的坐標;
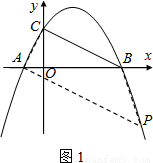
(3)在拋物線上存在點P,使得以A、C、B、P四點為頂點的四邊形是直角梯形,求出P點的坐標.
(1)y=-x2+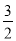 x+1;△ABC是直角三角形,且∠ACB=90°;(2)D(
x+1;△ABC是直角三角形,且∠ACB=90°;(2)D(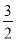 ,1);(3)P(
,1);(3)P(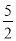 ,-
,-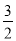 )或(-
)或(-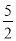 ,-9).
,-9).
【解析】
試題分析:(1)將A、B的坐標代入拋物線的解析式中即可確定拋物線的解析式;進而可得到C點坐標,進而可求出AC、BC、AB的長,然后再判斷△ABC的形狀;
(2)根據拋物線和等腰梯形的對稱性知,點C關于拋物線對稱軸的對稱點符合點D的要求,由此可求出點D的坐標;
(3)在(1)題已將證得∠ACB=90°,若A、C、B、P四點為頂點的四邊形是直角梯形,則有兩種情況需要考慮:
①以BC、AP為底,AC為高;可先求出直線BC的解析式,進而可確定直線AP的解析式,聯立拋物線的解析式即可求出點P的坐標.
②以AC、BP為底,BC為高;方法同①.
試題解析:(1)由題意得:
 ,
,
解得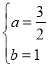 ;
;
∴拋物線的解析式為y=-x2+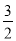 x+1;
x+1;
∴C(0,1);
∴AC2=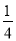 +1=
+1=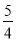 ,BC2=1+4=5,AB2=(2+
,BC2=1+4=5,AB2=(2+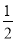 )2=
)2=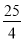 ;
;
∴AC2+BC2=AB2,即△ABC是直角三角形,且∠ACB=90°;
(2)由(1)的拋物線知:其對稱軸方程為x=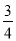 ;
;
根據拋物線和等腰梯形的對稱性知:點D(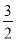 ,1);
,1);
(3)存在,點P(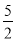 ,-
,-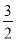 )或(-
)或(-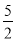 ,-9);
,-9);
若以A、C、B、P四點為頂點的直角梯形以BC、AP為底;
∵B(2,0),C(0,1),
∴直線BC的解析式為:y=-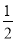 x+1;
x+1;
設過點A且平行于BC的直線的解析式為y=-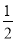 x+h,
x+h,
則有:(-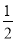 )×(-
)×(-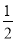 )+h=0,h=-
)+h=0,h=-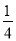 ;
;
∴y=-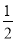 x-
x-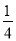 ;
;
聯立拋物線的解析式有:
 ,
,
解得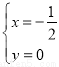 ,
,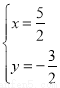 ;
;
∴點P(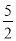 ,-
,-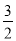 );
);
若以A、C、B、P四點為頂點的直角梯形以AC、BP為底,
同理可求得P(-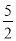 ,-9);
,-9);
故當P(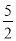 ,-
,-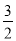 )或(-
)或(-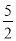 ,-9)時,以A、C、B、P四點為頂點的四邊形是直角梯形.
,-9)時,以A、C、B、P四點為頂點的四邊形是直角梯形.
(根據拋物線的對稱性求出另一個P點坐標亦可)
考點:二次函數綜合題.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數學 來源:2014-2015學年江蘇省興化顧莊三校八年級上學期12月月考數學試卷(解析版) 題型:解答題
(10分)如圖,是交警在一個路口統計的某個時段來往車輛的車速(單位:千米/時)情況.
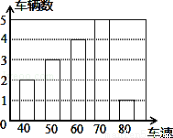
(1)計算這些車的平均速度;
(2)車速的眾數是多少?
(3)車速的中位數是多少?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省八年級上學期第二次月考數學試卷(解析版) 題型:選擇題
下列說法中錯誤的是( )
A.5是25的算術平方根
B.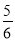 是
是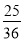 的一個平方根
的一個平方根
C.9的平方根是3
D.0的平方根與算術平方根都是0
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省濟南市九年級上學期期末競賽數學試卷(解析版) 題型:填空題
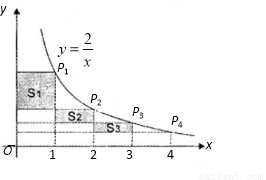
如圖,在反比例函數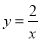 (
(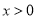 )的圖象上,有點
)的圖象上,有點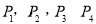 ,它們的橫坐標依次為1,2,3,4.分別過這些點作
,它們的橫坐標依次為1,2,3,4.分別過這些點作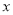 軸與
軸與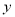 軸的垂線,圖中所構成的陰影部分的面積從左到右依次為
軸的垂線,圖中所構成的陰影部分的面積從左到右依次為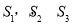 ,則
,則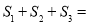 .
.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省濟南市九年級上學期期末競賽數學試卷(解析版) 題型:選擇題
把拋物線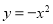 向左平移1個單位,然后向上平移3個單位,則平移后拋物線的解析式為( ). A.
向左平移1個單位,然后向上平移3個單位,則平移后拋物線的解析式為( ). A.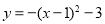
B.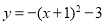
C.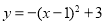
D.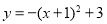
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省富陽市八年級10月月考數學試卷(解析版) 題型:解答題
(本小題滿分10分)如圖,已知O是線段AC、DB的交點,且AC=BD,AB=DC.求證:OB=OC.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省廣安岳池白廟責任區八年級12月聯考數學試卷(解析版) 題型:選擇題
已知實數a、b,若a>b,則下列結論正確的是( )
A.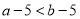 B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com