求值:①x2+3=3(x+1);
②4(3x+1)2=25(x-2)2.
【答案】
分析:(1)先將方程整理為一般形式后,發現可對方程提取公因式x,得到( )( )=0的形式,則這兩個相乘的數至少有一個為0,由此可以解出x的值.
(2)先移項,再運用平方差公式進行因式分解,由此可以解出x的值.
解答:解:①x
2+3=3(x+1)
x
2-3x=0
x(x-3)=0
解得:x
1=0,x
2=3.
②4(3x+1)
2=25(x-2)
2
4(3x+1)
2-25(x-2)
2=0
(6x+2+5x-10)(6x+2-5x+10)=0
(11x-8)(x+12)=0
解得:x
1=
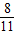
,x
2=-12.
點評:本題考查一元二次方程的解法.解一元二次方程常用的方法有直接開平方法,配方法,公式法,因式分解法,要根據方程的特點靈活選用合適的方法.

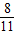 ,x2=-12.
,x2=-12.
