
【題目】在△ABC與△ABD中,∠DBA=∠CAB,AC與BD交于點F
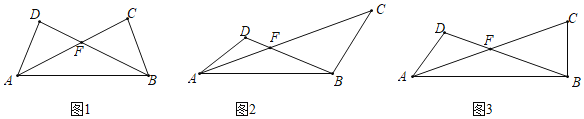
(1)如圖1,若∠DAF=∠CBF,求證:AD=BC;
(2)如圖2,∠D=135°,∠C=45°,AD=2,AC=4,求BD的長.
(3)如圖3,若∠DBA=18°,∠D=108°,∠C=72°,AD=1,直接寫出DB的長.
 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩個草莓采摘園為吸引顧客,在草莓銷售價格相同的基礎上分別推出優惠方案,甲園:顧客進園需購買門票,采摘的草莓按六折優惠.乙園:顧客進園免門票,采摘草莓超過一定數量后,超過的部分打折銷售.活動期間,某顧客的草莓采摘量為x kg,若在甲園采摘需總費用y1元,若在乙園采摘需總費用y2元, y1,y2與x之間的函數圖象如圖所示,則下列說法中錯誤的是( )
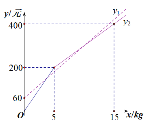
A.甲園的門票費用是60元
B.草莓優惠前的銷售價格是40元/kg
C.乙園超過5 kg后,超過的部分價格優惠是打五折
D.若顧客采摘12 kg草莓,那么到甲園或乙園的總費用相同
查看答案和解析>>
科目:初中數學 來源: 題型:
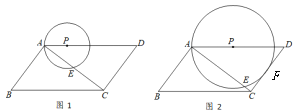
【題目】如圖1,平行四邊形ABCD中,AB⊥AC,AB=3,AD=5,點P在邊AD上運動,以P為圓心,PA為半徑的⊙P與對角線AC交于A,E兩點.
(1)如圖2,當⊙P與邊CD相切于點F時,求AP的長;
(2)不難發現,當⊙P與邊CD相切時,⊙P與平行四邊形ABCD的邊有三個公共點,隨著AP的變化,⊙P與平行四邊形ABCD的邊的公共點的個數也在變化,若公共點的個數為4,直接寫出相對應的AP的值的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
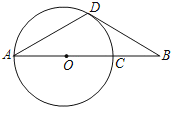
【題目】如圖,線段AB經過⊙O的圓心O,交⊙O于A、C兩點,BC=1,AD為⊙O的弦,連結BD,∠BAD=∠ABD=30°.
(1)求證:直線BD是⊙O的切線;
(2)求⊙O的半徑長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】只有1和它本身兩個因數且大于1的正整數叫做素數.我國數學家陳景潤哥德巴赫猜想的研究中取得了世界領先的成果.哥德巴赫猜想是“每個大于2的偶數都表示為兩個素數的和”,如10=3+7.
(1)從7,11,13,17這4個素數中隨機抽取一個,則抽到的數是11的概率是_____;
(2)從7,11,13,17這4個素數中隨機抽取1個數,再從余下的3個數中隨機抽取1個數,用畫樹狀圖或列表的方法,求抽到的兩個素數之和等于24的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A(-1.5,0),B(0,2),將△ABO順著x軸的正半軸無滑動的滾動,第一次滾動到①的位置,點B的對應點記作B1;第二次滾動到②的位置,點B1的對應點記作B2;第三次滾動到③的位置,點B2的對應點記作B3;![]() ;依次進行下去,則點B2020的坐標為__________.
;依次進行下去,則點B2020的坐標為__________.
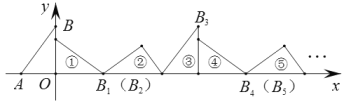
查看答案和解析>>
科目:初中數學 來源: 題型:
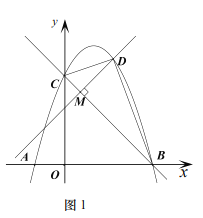
【題目】已知二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,點
點,點![]() 在直線
在直線![]() 上,橫坐標為
上,橫坐標為![]() .
.
(1)確定二次函數![]() 的解析式;
的解析式;
(2)如圖1,![]() 時,
時,![]() 交二次函數
交二次函數![]() 的圖象于點
的圖象于點![]() 的面積記作
的面積記作![]() 為何值時
為何值時![]() 的值最大,并求出
的值最大,并求出![]() 的最大值;
的最大值;
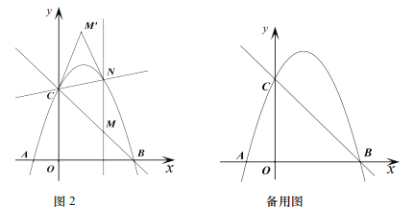
(3)如圖2,過點![]() 作
作![]() 軸的平行線交二次函數
軸的平行線交二次函數![]() 的圖象于點
的圖象于點![]() 點
點![]() 與點
與點![]() 關于直線
關于直線![]() 對稱是否存在點
對稱是否存在點![]() 使四邊形
使四邊形![]() 為菱形,若存在直接寫出
為菱形,若存在直接寫出![]() 的值;若不存在請說明理由.
的值;若不存在請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com