
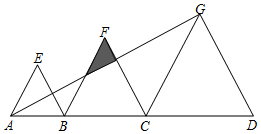
 如圖,點B、C是線段AD上的點,△ABE、△BCF、△CDG都是等邊三角形,且AB=4,BC=6,已知△ABE與△CDG的相似比為2:5.則
如圖,點B、C是線段AD上的點,△ABE、△BCF、△CDG都是等邊三角形,且AB=4,BC=6,已知△ABE與△CDG的相似比為2:5.則分析 ①利用相似三角形對應邊成比例列式計算即可得解;
②設AG與CF、BF分別相交于點M、N,根據等邊對等角求出∠CAG=∠CGA,再利用三角形的一個外角等于與它不相鄰的兩個內角的和求出∠CGA=30°,然后求出AG⊥GD,再根據相似三角形對應邊成比例求出CM,從而得到MF,然后求出MN,再利用三角形的面積公式列式計算即可得解.
解答 ①解:∵△ABE、△CDG都是等邊三角形,
∴△ABE∽△CDG,
∴$\frac{AB}{CD}$=$\frac{2}{5}$,
即$\frac{4}{CD}$=$\frac{2}{5}$,
解得CD=10;
②解:如圖,設AG與CF、BF分別相交于點M、N,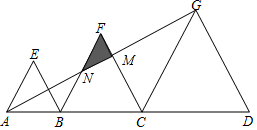
∵AC=AB+BC=4+6=10,
∴AC=CG,
∴∠CAG=∠CGA,
又∵∠CAG+∠CGA=∠DCG=60°,
∴∠CGA=30°,
∴∠AGD=∠CGA+∠CGD=30°+60°=90°,
∴AG⊥GD,
∵∠BCF=∠D=60°,
∴CF∥DG,
∴△ACM∽△ADG,
∴MN⊥CF,
$\frac{CM}{DG}$=$\frac{AC}{AD}$,
即$\frac{CM}{10}$=$\frac{10}{20}$,
解得CM=5,
所以,MF=CF-CM=6-5=1,
∵∠F=60°,
∴MN=$\sqrt{3}$MF=$\sqrt{3}$,
∴S△MNF=$\frac{1}{2}$MF•MN=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
即陰影部分面積為$\frac{\sqrt{3}}{2}$.
故答案為:10;$\frac{\sqrt{3}}{2}$.
點評 本題考查了相似三角線的判定與性質等邊三角形的性質,主要利用了相似三角形對應邊成比例的性質,難點在于②判斷出直角三角形.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖所示,四邊形OABC是矩形,點D在OC邊上,以AD為折痕,將△OAD向上翻折,點O恰好落在BC邊上的點E處,若△ECD的周長為4,△EBA的周長為12.
如圖所示,四邊形OABC是矩形,點D在OC邊上,以AD為折痕,將△OAD向上翻折,點O恰好落在BC邊上的點E處,若△ECD的周長為4,△EBA的周長為12.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com