
 如圖,已知直線l1:y=-$\frac{3}{4}$x+6與x軸交于點A,與y軸交于點B,將直線l1向下平移4個單位長度后得到直線l2,直線l2與x軸交于點C,與y軸交于點D.
如圖,已知直線l1:y=-$\frac{3}{4}$x+6與x軸交于點A,與y軸交于點B,將直線l1向下平移4個單位長度后得到直線l2,直線l2與x軸交于點C,與y軸交于點D.分析 (1)分別令y=-$\frac{3}{4}$x+6中x、y=0求出與之對應(yīng)的y、x的值,由此即可得出點B、A的坐標(biāo),再根據(jù)三角形的面積公式即可求出△AOB的面積;
(2)根據(jù)直線l1的函數(shù)表達式結(jié)合“上加下減”的平移規(guī)則即可得出直線l2的函數(shù)表達式;
(3)根據(jù)直線l2的函數(shù)表達式利用一次函數(shù)圖象上點的坐標(biāo)特征即可求出點C、D的坐標(biāo),進而即可求出S四邊形ABCD的值,設(shè)點P的橫坐標(biāo)為m(0<m≤8),根據(jù)三角形的面積公式結(jié)合S△PBD=$\frac{1}{2}$S四邊形ABCD即可得出關(guān)于m的一元一次方程,解之可得出m的值,再根據(jù)m的值利用一次函數(shù)圖象上點的坐標(biāo)特征即可得出點P的坐標(biāo).
解答 解:(1)當(dāng)x=0時,y=-$\frac{3}{4}$x+6=6,
∴點B的坐標(biāo)為(0,6);
當(dāng)y=-$\frac{3}{4}$x+6=0時,x=8,
∴點A的坐標(biāo)為(8,0).
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×8×6=24.
(2)∵將直線l1向下平移4個單位長度后得到直線l2,
∴直線l2的函數(shù)表達式是y=-$\frac{3}{4}$x+6-4=-$\frac{3}{4}$x+2.
故答案為:y=-$\frac{3}{4}$x+2.
(3)當(dāng)x=0時,y=-$\frac{3}{4}$x+2=2,
∴點D的坐標(biāo)為(0,2);
當(dāng)y=-$\frac{3}{4}$x+2=0時,x=$\frac{8}{3}$,
∴點C的坐標(biāo)為($\frac{8}{3}$,0).
∴S四邊形ABCD=S△AOB-S△COD=24-$\frac{1}{2}$×2×$\frac{8}{3}$=$\frac{64}{3}$.
設(shè)點P的橫坐標(biāo)為m(0<m≤8),
∵S△PBD=$\frac{1}{2}$S四邊形ABCD,
∴BD•m=(6-2)m=$\frac{64}{3}$,
解得:m=$\frac{16}{3}$,
∵$\frac{8}{3}$<$\frac{16}{3}$<8,且當(dāng)x=$\frac{16}{3}$時,y=-$\frac{3}{4}$x+6=-$\frac{3}{4}$×$\frac{16}{3}$+6=2,
∴點P的坐標(biāo)為($\frac{16}{3}$,0)和($\frac{16}{3}$,2).
點評 本題考查了一次函數(shù)圖象與幾何變換、一次函數(shù)圖象上點的坐標(biāo)特征、三角形的面積以及解一元一次方程,熟練掌握圖形平移的規(guī)律“上加下減,左加右減”是解題的關(guān)鍵.


 單元加期末復(fù)習(xí)先鋒大考卷系列答案
單元加期末復(fù)習(xí)先鋒大考卷系列答案 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,已知正方形ABCD,頂點A(1,3)、B(1,1)、C(3,1)規(guī)定“把正方形ABCD先沿x軸翻折,再向左平移1個單位”為一次變換,如此這樣,連續(xù)經(jīng)過2017次變換后,正方形ABCD的對角線交點M的坐標(biāo)變?yōu)椋ā 。?table class="qanwser">
如圖,已知正方形ABCD,頂點A(1,3)、B(1,1)、C(3,1)規(guī)定“把正方形ABCD先沿x軸翻折,再向左平移1個單位”為一次變換,如此這樣,連續(xù)經(jīng)過2017次變換后,正方形ABCD的對角線交點M的坐標(biāo)變?yōu)椋ā 。?table class="qanwser">查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
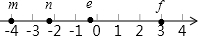 有理數(shù)m,n,e,f在數(shù)軸上的對應(yīng)點的位置如圖所示,這四個數(shù)中,絕對值最小的是( )
有理數(shù)m,n,e,f在數(shù)軸上的對應(yīng)點的位置如圖所示,這四個數(shù)中,絕對值最小的是( )| A. | m | B. | n | C. | e | D. | f |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
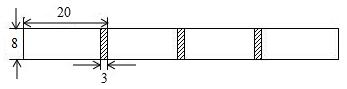
| 白紙張數(shù)x(張) | 1 | 2 | 3 | 4 | 5 | … |
| 紙條長度y(cm) | 20 | 37 | 54 | 71 | 88 | … |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com