在平面直角坐標系xOy中，對于點P（x，y），我們把點P（﹣y+1，x+1）叫做點P的伴隨點．已知點A1的伴隨點為A2，點A2的伴隨點為A3，點A3的伴隨點為A4，…，這樣依次得到點A1，A2，A3，…，An，…．若點A1的坐標為（3，1），則點A3的坐標為 ，點A2014的坐標為 ；若點A1的坐標為（a，b），對于任意的正整數n，點An均在x軸上方，則a，b應滿足的條件為 ．
（﹣3，1）（0，4）﹣1＜a＜1且0＜b＜2
解：∵A1的坐標為（3，1），
∴A2（0，4），A3（﹣3，1），A4（0，﹣2），A5（3，1），
…，
依此類推，每4個點為一個循環(huán)組依次循環(huán)，
∵2014÷4=503余2，
∴點A2014的坐標與A2的坐標相同，為（0，4）；
∵點A1的坐標為（a，b），
∴A2（﹣b+1，a+1），A3（﹣a，﹣b+2），A4（b﹣1，﹣a+1），A5（a，b），
…，
依此類推，每4個點為一個循環(huán)組依次循環(huán)，
∵對于任意的正整數n，點An均在x軸上方，
∴
，
，
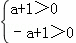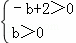解得﹣1＜a＜1，0＜b＜2
科目：初中數學 來源： 題型：
如圖，在△ABC中，點D在邊AB上，BD=2AD，DE∥BC交AC于點E，若線段DE=5，則線段BC的長為（ ）
|
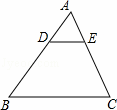
| A． | 7.5 | B． | 10 | C． | 15 | D． | 20 |
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖1，在平面直角坐標系中，二次函數y=﹣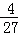
x2+12的圖象與y軸交于點A，與x軸交于B，C兩點（點B在點C的左側），連接AB，AC．
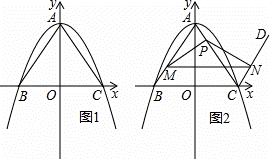
（1）點B的坐標為 ，點C的坐標為 ；
（2）過點C作射線CD∥AB，點M是線段AB上的動點，點P是線段AC上的動點，且始終滿足BM=AP（點M不與點A，點B重合），過點M作MN∥BC分別交AC于點Q，交射線CD于點N （點 Q不與點P重合），連接PM，PN，設線段AP的長為n．
①如圖2，當n＜
AC時，求證：△PAM≌△NCP；
②直接用含n的代數式表示線段PQ的長；
③若PM的長為
，當二次函數y=﹣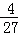x2+12的圖象經過平移同時過點P和點N時，請直接寫出此時的二次函數表達式．
查看答案和解析>>
科目：初中數學 來源： 題型：
正方形ABCD外側作直線AP，點B關于直線AP的對稱點為E，連接BE，DE，其中DE交直線AP于點F．
（1）依題意補全圖1；
（2）若∠PAB=20°，求∠ADF的度數；
（3）如圖2，若45°＜∠PAB＜90°，用等式表示線段AB，F(xiàn)E，F(xiàn)D之間的數量關系，并證明．
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
