
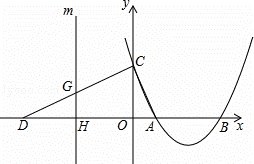
如圖,拋物線y=ax2﹣8ax+12a(a>0)與x軸交于A、B兩點(A在B的左側),與y軸交于點C,點D的坐標為(﹣6,0),且∠ACD=90°.
(1)請直接寫出A、B兩點的坐標;
(2)求拋物線的解析式;
(3)拋物線的對稱軸上是否存在點P,使得△PAC的周長最小?若存在,求出點P的坐標及周長的最小值;若不存在,說明理由;
(4)平行于y軸的直線m從點D出發沿x軸向右平行移動,到點A停止.設直線m與折線DCA的交點為G,與x軸的交點為H(t,0).記△ACD在直線m左側部分的面積為s,求s關于t的函數關系式及自變量t的取值范圍.
解:(1)拋物線的解析式為:y=ax2﹣8ax+12a(a>0),
令y=0,即ax2﹣8ax+12a=0,
解得x1=2,x2=6,
∴A(2,0),B(6,0).
(2)拋物線的解析式為:y=ax2﹣8ax+12a(a>0),
令x=0,得y=12a,∴C(0,12a),OC=12a.
在Rt△COD中,由勾股定理得:CD2=OC2+OD2=(12a)2+62=144a2+36;
在Rt△COD中,由勾股定理得:AC2=OC2+OA2=(12a)2+22=144a2+4;
在Rt△COD中,由勾股定理得:DC2+AC2=AD2;
即:(144a2+36)+(144a2+4)=82,
解得:a=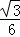 或a=﹣
或a=﹣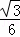 (舍去),
(舍去),
∴拋物線的解析式為:y=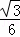 x2﹣
x2﹣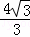 x+
x+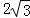 .
.
(3)存在.
對稱軸為直線:x=﹣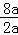 =4.
=4.
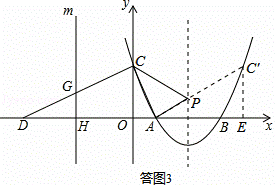
由(2)知C(0,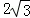 ),則點C關于對稱軸x=4的對稱點為C′(8,
),則點C關于對稱軸x=4的對稱點為C′(8,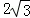 ),
),
連接AC′,與對稱軸交于點P,則點P為所求.此時△PAC周長最小,最小值為AC+AC′.
設直線AC′的解析式為y=kx+b,則有:
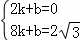 ,解得
,解得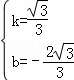 ,
,
∴y=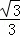 x﹣
x﹣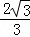 .
.
當x=4時,y=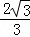 ,∴P(4,
,∴P(4,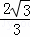 ).
).
過點C′作C′E⊥x軸于點E,則C′E=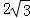 ,AE=6,
,AE=6,
在Rt△AC′E中,由勾股定理得:AC′=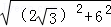 =4
=4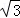 ;
;
在Rt△AOC中,由勾股定理得:AC=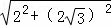 =4.
=4.
∴AC+AC′=4+4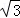 .
.
∴存在滿足條件的點P,點P坐標為(4,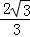 ),△PAC周長的最小值為4+4
),△PAC周長的最小值為4+4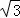 .
.
(4)①當﹣6≤t≤0時,如答圖4﹣1所示.
∵直線m平行于y軸,
∴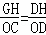 ,即
,即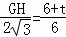 ,解得:GH=
,解得:GH=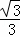 (6+t)
(6+t)
∴S=S△DGH=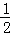 DH•GH=
DH•GH=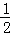 (6+t)•
(6+t)•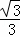 (6+t)=
(6+t)=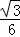 t2+2
t2+2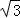 t+6
t+6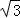 ;
;
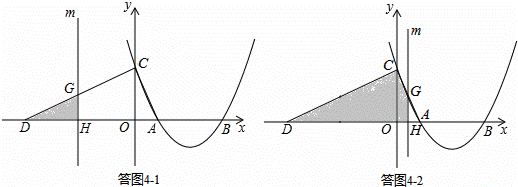
②當0<t≤2時,如答圖4﹣2所示.
∵直線m平行于y軸,
∴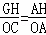 ,即
,即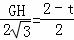 ,解得:GH=﹣
,解得:GH=﹣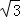 t+2
t+2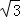 .
.
∴S=S△COD+S梯形OCGH=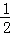 OD•OC+
OD•OC+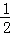 (GH+OC)•OH
(GH+OC)•OH
=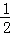 ×6×2
×6×2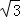 +
+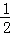 (﹣
(﹣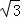 t+2
t+2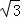 +2
+2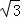 )•t
)•t
=﹣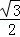 t2+2
t2+2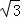 t+6
t+6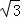 .
.
∴S=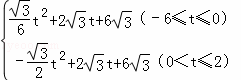 .
.


 口算題天天練系列答案
口算題天天練系列答案科目:初中數學 來源: 題型:
在某市開展的“讀中華經典,做書香少年”讀書月活動中,圍繞學生日人均閱讀時間這一問題,對初二學生進行隨機抽樣調查.如圖是根據調查結果繪制成的統計圖(不完整),請你根據圖中提供的信息解答下列問題: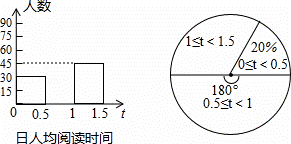
(1)本次抽樣調查的樣本容量是多少?
(2)請將條形統計圖補充完整.
(3)在扇形統計圖中,計算出日人均閱讀時間在1~1.5小時對應的圓心角度數.
(4)根據本次抽樣調查,試估計該市12000名初二學生中日人均閱讀時間在0.5~1.5小時的多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,在梯形OABC中,OC∥AB,OA=CB,點O為坐標原點,且A(2,﹣3),C(0,2).
(1)求過點B的雙曲線的解析式;
(2)若將等腰梯形OABC向右平移5個單位,問平移后的點C是否落在(1)中的雙曲線上?并簡述理由.
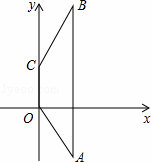
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com