
【題目】第二屆“一帶一路”國際合作高峰論壇將于2019年4月在北京舉行.為了讓恩施特產走出大山,走向世界,恩施一民營企業計劃生產甲、乙兩種商品共10萬件,銷住“一帶一路”沿線國家和地區.已知3件甲種商品與2件乙種商品的銷售收入相同,1件甲種商品比2件乙種商品的銷售收入少600元.甲、乙兩種商品的銷售利潤分別為120元和200元
(1)甲、乙兩種商品的銷售單價各多少元?
(2)市場調研表明:所有商品能全部售出,企業要求生產乙種商品的數量不超過甲種商品數量的![]() ,且甲、乙兩種商品的銷售總收入不低于3300萬元,請你為該企業設計一種生產方案,使銷售總利潤最大.
,且甲、乙兩種商品的銷售總收入不低于3300萬元,請你為該企業設計一種生產方案,使銷售總利潤最大.
【答案】(1)甲種商品的銷售單價是300元,乙種商品的單價為450元;(2)該企業生產甲種商品6萬件,則生產乙種商品4萬件時銷售總利潤最大,最大利潤為15200000元.
【解析】
(1)可設甲種商品的銷售單價x元,乙種商品的銷售單價y元,根據等量關系:①3件甲種商品與2件乙種商品的銷售收入相同,②1件甲種商品比2件乙種商品的銷售收入少600元,列出方程組求解即可;
(2)可設生產甲種商品a萬件,根據“生產乙種商品的數量不超過甲種商品數量的![]() ,且甲、乙兩種商品的銷售總收入不低于3300萬元”,列出不等式組求解即可.
,且甲、乙兩種商品的銷售總收入不低于3300萬元”,列出不等式組求解即可.
解:(1)設甲種商品的銷售單價x元,乙種商品的銷售單價y元,依題意有
![]() ,
,
解得![]() ,
,
答:甲種商品的銷售單價是300元,乙種商品的單價為450元;
(2)設生產甲種商品a萬件,則生產乙種商品(10﹣a)萬件,根據題意得
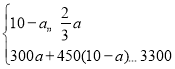 ,
,
解得6≤a≤8,
∵乙種商品的銷售利潤比甲種商品的銷售利潤高,
∴乙種商品銷售越多,銷售總利潤就越大,
∴當生產甲種商品6萬件,則生產乙種商品4萬件時銷售總利潤最大.此時銷售總利潤為:60000×120+40000×200=15200000(元).
答:該企業生產甲種商品6萬件,則生產乙種商品4萬件時銷售總利潤最大,最大利潤為15200000元.


 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:初中數學 來源: 題型:
【題目】在菱形![]() 中,對角線
中,對角線![]() 與
與![]() 交于點
交于點![]() ,
,![]() ,
,![]() ,點
,點![]() 是對角線
是對角線![]() 上一點(可與
上一點(可與![]() ,
,![]() 重合),以點
重合),以點![]() 為圓心,
為圓心,![]() 為半徑作
為半徑作![]() (其中
(其中![]() ).
).
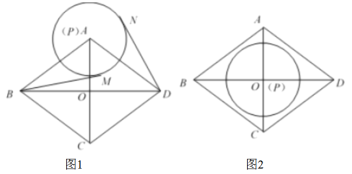
(1)如圖1,當點![]() 與
與![]() 重合,且
重合,且![]() 時,過點
時,過點![]() ,
,![]() 分別作
分別作![]() 的切線,切點分別為
的切線,切點分別為![]() ,
,![]() .求證:
.求證:![]() ;
;
(2)如圖2,當點![]() 與點
與點![]() 重合,且
重合,且![]() 在菱形
在菱形![]() 內部時(不含邊界),求
內部時(不含邊界),求![]() 的取值范圍;
的取值范圍;
(3)當點![]() 為
為![]() 或
或![]() 的內心時,直接寫出
的內心時,直接寫出![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
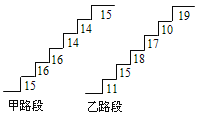
【題目】在某旅游景區上山的一條小路上,有一些斷斷續續的臺階,下圖是其中的甲、乙兩段臺階的示意圖,圖中的數字表示每一級臺階的高度(單位:cm).請你用所學過的有關統計知識,回答下列問題(數據:15,16,16,14,14,15的方差![]() ,數據:11,15,18,17,10,19的方差
,數據:11,15,18,17,10,19的方差![]() :
:
(1)分別求甲、乙兩段臺階的高度平均數;
(2)哪段臺階走起來更舒服?與哪個數據(平均數、中位數、方差和極差)有關?
(3)為方便游客行走,需要陳欣整修上山的小路,對于這兩段臺階路.在總高度及臺階數不變的情況下,請你提出合理的整修建議.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了創建國家級衛生城區,某社區在九月份購買了甲、乙兩種綠色植物共1100盆,共花費了27000元.已知甲種綠色植物每盆20元,乙種綠色植物每盆30元.
(1)該社區九月份購買甲、乙兩種綠色植物各多少盆?
(2)十月份,該社區決定再次購買甲、兩種綠色植物.已知十月份甲種綠色植物每盆的價格比九月份的價格優惠![]() 元
元![]() ,十月份乙種綠色植物每盆的價格比九月份的價格優惠
,十月份乙種綠色植物每盆的價格比九月份的價格優惠![]() .因創衛需要,該社區十月份購買甲種綠色植物的數量比九月份的數量增加了
.因創衛需要,該社區十月份購買甲種綠色植物的數量比九月份的數量增加了![]() ,十為份購買乙種綠色植物的數量比九月份的數量增加了
,十為份購買乙種綠色植物的數量比九月份的數量增加了![]() .若該社區十月份的總花費與九月份的總花費恰好相同,求
.若該社區十月份的總花費與九月份的總花費恰好相同,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
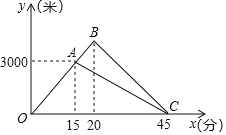
【題目】張琪和爸爸到曲江池遺址公園運動,兩人同時從家出發,沿相同路線前行,途中爸爸有事返回,張琪繼續前行5分鐘后也原路返回,兩人恰好同時到家張琪和爸爸在整個運動過程中離家的路點y1(米),y2(米)與運動時間x(分)之間的函數關系如圖所示
(1)求爸爸返問時離家的路程y2(米)與運動時間x(分)之間的函數關系式;
(2)張琪開始返回時與爸爸相距多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(感知)“如圖①,![]() ,
,![]() 平分
平分![]() ,作
,作![]() ,
,![]() 、
、![]() 分別交射線
分別交射線![]() 、
、![]() 于
于![]() 、
、![]() 兩點,連結
兩點,連結![]() ,求
,求![]() 的度數”為了求解問題,某同學做了如下的分析,
的度數”為了求解問題,某同學做了如下的分析,
“過點![]() 作
作![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,”進而求解,則
,”進而求解,則![]() ________
________![]() .
.
(拓展)如圖②,一般地,設![]()
![]() ,
,![]() 平分
平分![]() ,作
,作![]() ,
,![]() 、
、![]() 分別交射線
分別交射線![]() 、
、![]() 于
于![]() 、
、![]() 兩點,連結
兩點,連結![]() .
.
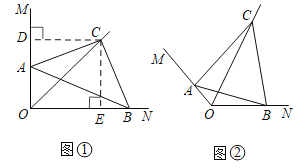
(1)求![]() 的度數.(用含
的度數.(用含![]() 的代數式表示)
的代數式表示)
(2)若![]() ,
,![]() ,
,![]() ,則
,則![]() ________.
________.
查看答案和解析>>
科目:初中數學 來源: 題型:
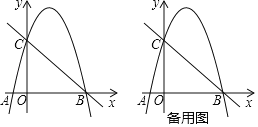
【題目】如圖,二次函數y=ax2﹣3ax+c的圖象與x軸交于點A、B,與y軸交于點C直線y=﹣x+4經過點B、C.
(1)求拋物線的表達式;
(2)過點A的直線交拋物線于點M,交直線BC于點N.
①點N位于x軸上方時,是否存在這樣的點M,使得AM:NM=5:3?若存在,求出點M的坐標;若不存在,請說明理由.
②連接AC,當直線AM與直線BC的夾角∠ANB等于∠ACB的2倍時,請求出點M的橫坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
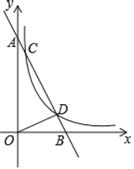
【題目】如圖,在平面直角坐標系中,直線AB與x軸交于點B,與y軸交于點A,直線AB與反比例函數y=![]() (m>0)在第一象限的圖象交于點C、點D,其中點C的坐標為(1,8),點D的坐標為(4,n).
(m>0)在第一象限的圖象交于點C、點D,其中點C的坐標為(1,8),點D的坐標為(4,n).
(1)分別求m、n的值;
(2)連接OD,求△ADO的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com