

分析 (1)根據兩條直線AB,CD相交于點O,∠AOC=∠AOD,可得圖中一定有4個直角;當t=2時,可求得∠MON的度數和∠BON的度數;
(2)根據OE平分∠COM,OF平分∠NOD,求得∠COE=$\frac{1}{2}$∠COM=$\frac{1}{2}$(15t-90°),∠DOF=$\frac{1}{2}$∠DON=$\frac{1}{2}$×12t,再根據當∠EOF為直角時,∠COE+∠DOF=90°,列出方程$\frac{1}{2}$(15t-90°)=$\frac{1}{2}$×12t,解得t的值為10s;
(3)先判斷當射線OM在∠COB內部,∠MON為平角,∠MOB為直角時t的值,再以此分兩種情況討論:當0<t<$\frac{10}{3}$時,當$\frac{10}{3}$<t<6時,分別計算$\frac{7∠COM+2∠BON}{∠MON}$的值,根據結果作出判斷即可.
解答 解:(1)如圖所示,∵兩條直線AB,CD相交于點O,∠AOC=∠AOD,
∴∠AOC=∠AOD=90°,
∴∠BOC=∠BOD=90°,
∴圖中一定有4個直角;
當t=2時,∠BOM=30°,∠NON=24°,
∴∠MON=30°+90°+24°=144°,
∠BON=90°+24°=114°;
故答案為:4;144°,114°;
(2)如圖所示,∠BOM=15t,∠NON=12t,∠COM=15t-90°,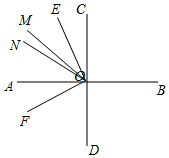
∵OE平分∠COM,OF平分∠NOD,
∴∠COE=$\frac{1}{2}$∠COM=$\frac{1}{2}$(15t-90°),∠DOF=$\frac{1}{2}$∠DON=$\frac{1}{2}$×12t,
∵當∠EOF為直角時,∠COE+∠DOF=90°,
∴$\frac{1}{2}$(15t-90°)=$\frac{1}{2}$×12t,
解得t=10,
∴當∠EOF為直角時,t的值為10s;
(3)當∠MON=180°時,∠BOM+∠BOD+∠DON=180°,
∴15t+90°+12t=180°,
解得t=$\frac{10}{3}$,
當∠BOM=90°時,15t=90°,
解得t=6,
①如圖所示,當0<t<$\frac{10}{3}$時,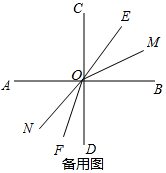
∠COM=90°-15t,∠BON=90°+12t,
∠MON=∠BOM+∠BOD+∠DON=15t+90°+12t,
∴$\frac{7∠COM+2∠BON}{∠MON}$=$\frac{7(90°-15t)+2(90°+12t)}{15t+90°+12t}$=$\frac{810°-81t}{27t+90°}$,(不是定值)
②如圖所示,當$\frac{10}{3}$<t<6時,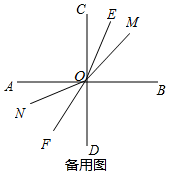
∠COM=90°-15t,∠BON=90°+12t,
∠MON=360°-(∠BOM+∠BOD+∠DON)=360°-(15t+90°+12t)=270°-27t,
∴$\frac{7∠COM+2∠BON}{∠MON}$=$\frac{7(90°-15t)+2(90°+12t)}{270°-27t}$=$\frac{810°-81t}{270°-27t}$=3,(是定值)
綜上所述,當射線OM在∠COB內部,且$\frac{7∠COM+2∠BON}{∠MON}$是定值時,t的取值范圍為$\frac{10}{3}$<t<6,這個定值是3.
點評 本題屬于幾何變換綜合題,主要考查了角的和差關系的計算,解決問題的關鍵是將相關的角用含t的代數式表示出來,并根據題意列出方程進行求解,以及進行分類討論,解題時注意方程思想和分類思想的靈活運用.


科目:初中數學 來源: 題型:選擇題
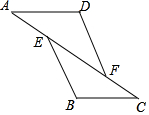 如圖,已知AE=CF,∠A=∠C,那么添加下列一個條件后,仍無法判定△ADF≌△CBE的是( )
如圖,已知AE=CF,∠A=∠C,那么添加下列一個條件后,仍無法判定△ADF≌△CBE的是( )| A. | ∠D=∠B | B. | BE=DF | C. | AD=CB | D. | BE∥DF |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,若有理數a、b在數軸上的對應點的位置如圖所示,則下列各式錯誤的是( )
如圖,若有理數a、b在數軸上的對應點的位置如圖所示,則下列各式錯誤的是( )| A. | $\frac{|a|}{a}$+$\frac{|b|}{b}$=0 | B. | a+b<0 | C. | |a+b|-a=b | D. | -b<a<-a<b |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,把“QQ”笑臉放在直角坐標系中,已知右眼A的坐標是(-2,3),嘴唇C點的坐標為(-1,1),則此“QQ”笑臉左眼B的坐標是( )
如圖,把“QQ”笑臉放在直角坐標系中,已知右眼A的坐標是(-2,3),嘴唇C點的坐標為(-1,1),則此“QQ”笑臉左眼B的坐標是( )| A. | (0,3) | B. | (0,1) | C. | (-1,2) | D. | (-1,3) |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 等于7 | B. | 小于7 | C. | 不小于7 | D. | 不大于7 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com