
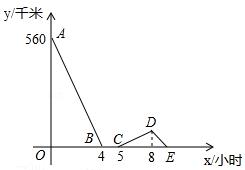
.一輛慢車與一輛快車分別從甲、乙兩地同時出發(fā),勻速相向而行,兩車在途中相遇后都停留一段時間,然后分別按原速一同駛往甲地后停車.設(shè)慢車行駛的時間為x小時,兩車之間的距離為y千米,圖中折線表示y與x之間的函數(shù)圖象,請根據(jù)圖象解決下列問題:
(1)甲乙兩地之間的距離為 千米;
(2)求快車和慢車的速度;
(3)求線段DE所表示的y與x之間的函數(shù)關(guān)系式,并寫出自變量x的取值范圍.

.解:(1)由題意可得出:甲乙兩地之間的距離為560千米;故答案為:560;
(2)由題意可得出:慢車往返分別用了4小時,慢車行駛4小時的距離,快車3小時即可行駛完,
∴設(shè)慢車速度為3xkm/h,快車速度為4xkm/h,
∵由題意可得出:快車行駛?cè)逃昧?小時,∴快車速度為: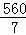 =80(km/h),
=80(km/h),
∴慢車速度為:80×=60(km/h),
(3)由題意可得出:當(dāng)行駛7小時后,慢車距離甲地60km,∴D(8,60),
∵慢車往返各需4小時,∴E(9,0),設(shè)DE的解析式為:y=kx+b,∴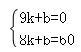 ,解得:
,解得: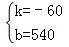 .
.
∴線段DE所表示的y與x之間的函數(shù)關(guān)系式為:y=﹣60x+540(8≤x≤9).


科目:初中數(shù)學(xué) 來源: 題型:
閱讀題例,解答下題:
例解方程x2﹣|x﹣1|﹣1=0
解:
(1)當(dāng)x﹣1≥0,即x≥1時x2﹣(x﹣1)﹣1=0x2﹣x=0
(2)當(dāng)x﹣1<0,即x<1時x2+(x﹣1)﹣1=0x2+x﹣2=0
解得:x1=0(不合題設(shè),舍去),x2=1
解得x1=1(不合題設(shè),舍去)x2=﹣2
綜上所述,原方程的解是x=1或x=﹣2
依照上例解法,解方程x2+2|x+2|﹣4=0.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
對于反比例函數(shù)y=
 ,下列說法正確的是( )
,下列說法正確的是( )
A.當(dāng)x>0時,y隨x的增大而增大 B.當(dāng)x<0時,y隨x的增大而增大
C.當(dāng)x<0時,y隨x的增大而減小 D.y隨x的增大而減小
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
某校校園超市老板到批發(fā)中心選購甲、乙兩種品牌的文具盒,乙品牌的進貨單價是甲品牌進貨單價的2倍,考慮各種因素,預(yù)計購進乙品牌文具盒的數(shù)量y(個)與甲品牌文具盒的數(shù)量x(個)之間的函數(shù)關(guān)系如圖所示.當(dāng)購進的甲、乙品牌的文具盒中,甲有120個時,購進甲、乙品牌文具盒共需7200元.
(1)根據(jù)圖象,求y與x之間的函數(shù)關(guān)系式;
(2)求甲、乙兩種品牌的文具盒進貨單價;
(3)若該超市每銷售1個甲種品牌的文具盒可獲利4元,每銷售1個乙種品牌的文具盒可獲利9元,根據(jù)學(xué)生需求,超市老板決定,準(zhǔn)備用不超過6300元購進甲、乙兩種品牌的文具盒,且這兩種品牌的文具盒全部售出后獲利不低于1795元,問該超市有幾種進貨方案?哪種方案能使獲利最大?最大獲利為多少元?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
已知 ,當(dāng)t=1時,S=13;當(dāng)t=2時,S=42,則當(dāng)t=3時,S等于( . )
,當(dāng)t=1時,S=13;當(dāng)t=2時,S=42,則當(dāng)t=3時,S等于( . )
A.106.5 B.87 C.70.5 D.69
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
某農(nóng)戶計劃購買甲、乙兩種油茶樹苗共1000株.已知乙種樹苗比甲種樹苗每株貴3元,且用100元錢購買甲種樹苗的株數(shù)與用160元錢購買乙種樹苗的株數(shù)剛好相同.
(1)求甲、乙兩種油茶樹苗每株的價格;
(2)如果購買兩種樹苗共用5600元,那么甲、乙兩種樹苗各買了多少株?
(3)調(diào)查統(tǒng)計得,甲、乙兩種樹苗的成活率分別為90%,95%.要使這批樹苗的成活率不低于92%,且使購買樹苗的費用最低,應(yīng)如何選購樹苗?最低費用是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
山地自行車越來越受到中學(xué)生的喜愛,各種品牌相繼投放市場,某車行經(jīng)營的A型車去年銷售總額為5萬元,今年每輛銷售價比去年降低400元,若賣出的數(shù)量相同,銷售總額將比去年減少20%.
(1)今年A型車每輛售價多少元?(用列方程的方法解答)
(2)該車計劃新進一批A型車和新款B型車共60輛,且B型車的進貨數(shù)量不超過A型車數(shù)量的兩倍,應(yīng)如何進貨才能使這批車獲利最多?
A,B兩種型號車的進貨和銷售價格如下表:

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
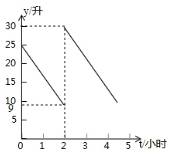
張師傅駕車從甲地到乙地,兩地相距500千米,汽車出發(fā)前油箱有油25升,途中加油若干升,加油前、后汽車都以100千米/小時的速度勻速行駛,已知油箱中剩余油量y(升)與行駛時間t(小時)之間的關(guān)系如圖所示.以下說法錯誤的是( )
A.加油前油箱中剩余油量y(升)與行駛時間t(小時)的函數(shù)關(guān)系是y=﹣8t+25
B.途中加油21升
C.汽車加油后還可行駛4小時
D.汽車到達乙地時油箱中還余油6升
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com