
 如圖,在平面直角坐標系中,二次函數y=x2+bx+c的圖象與x軸交于A、B兩點,A點在原點的左側,B點的坐標為(3,0),與y軸交于C(0,-3)點.
如圖,在平面直角坐標系中,二次函數y=x2+bx+c的圖象與x軸交于A、B兩點,A點在原點的左側,B點的坐標為(3,0),與y軸交于C(0,-3)點.分析 (1)點在拋物線上,將點的坐標代入即可求得拋物線解析式;
(2)根據圖形的關系,找出△BCD的面積為直角梯形面積減去兩個直角三角形的面積,套入坐標即可求得;
(3)由題意巧設坐標,用未知數m表示出來MN的長度,根據二次函數極值問題即可解決問題.
解答 解:(1)將B(3,0),C(0,-3)兩點的坐標代入得:$\left\{\begin{array}{l}{c=-3}\\{9+3b+c=0}\end{array}\right.$,
解得:b=-2,c=-3,
所以二次函數的表達式為:y=x2-2x-3.
(2)由y=(x-1)2-4得頂點D(1,-4),過D點做DP⊥y軸,垂足為點P,則P(0,-4),如圖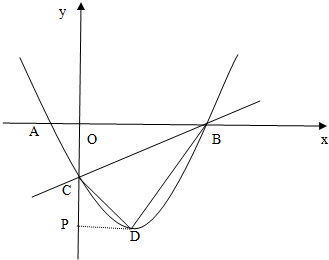
四邊形DPOB為直角梯形,△BOC與△DPC均為直角三角形,
△BCD的面積=梯形DPOB的面積-△BOC的面積-△DPC的面積
=$\frac{1}{2}$(OB+PD)×OP-$\frac{1}{2}$PC×PD-$\frac{1}{2}$CO×OB
又∵O(0,0),C(0,-3),B(3,0),D(1,-4),P(0,-4),
∴△BCD的面積=$\frac{1}{2}$×(1+3)×4-$\frac{1}{2}$×1×1-$\frac{1}{2}$×3×3=3.
(3)設直線BC的關系式為y=kx+n,
將B(3,0),C(0,-3)代入y=kx+n得
$\left\{\begin{array}{l}{n=-3}\\{3k+n=0}\end{array}\right.$,解得k=1,n=-3,
∴直線BC的關系式為y=x-3.
設M(m,m2-2m-3),則N(m,m-3),
∴MN=m-3-(m2-2m-3)=-m2+3m=-${(m-\frac{3}{2})}^{2}$+$\frac{9}{4}$
∴當m=$\frac{3}{2}$時,線段MN長度有最大值$\frac{9}{4}$,此時M的坐標為($\frac{3}{2}$,-$\frac{15}{4}$).
點評 本題考查了二次函數的綜合應用,解題的關鍵是學會拆分法求圖形面積,并會借助二次函數求極值來解決問題.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知雙曲線y=$\frac{k}{x}$上有兩點A(-1,-2),B(1,a),直線y=-x+a,P是雙曲線第一象限上一動點.
已知雙曲線y=$\frac{k}{x}$上有兩點A(-1,-2),B(1,a),直線y=-x+a,P是雙曲線第一象限上一動點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
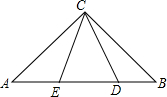 如圖,在Rt△ABC中,AC=BC,點D,E在斜邊AC上,且滿足AE=4,BD=3,∠DCE=45°,則DE的長度為( )
如圖,在Rt△ABC中,AC=BC,點D,E在斜邊AC上,且滿足AE=4,BD=3,∠DCE=45°,則DE的長度為( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖所示,AB,AC,BC是某公園三條兩兩相交的小路,管理人員為了方便游人休息,打算修建一個小亭子,使小亭子到三條小路的距離相等.請你用尺規為工作人員選好位置(要求:設計兩種方案工工作人員選擇)
如圖所示,AB,AC,BC是某公園三條兩兩相交的小路,管理人員為了方便游人休息,打算修建一個小亭子,使小亭子到三條小路的距離相等.請你用尺規為工作人員選好位置(要求:設計兩種方案工工作人員選擇)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com