【題目】用配方法將關于
的方程
可以變形為
，那么用配方法也可以將關于的方程
變形為下列形式（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
把關于x的方程x2+5x+n=0常數項n移項后，應該在左右兩邊同時加上一次項系數5的一半的平方可以求得n、p的值，然后用同樣的方法對關于x的方程x2-5x+n=-1進行變形．
把方程x2+5x+n=0的常數項移到等號的右邊,得到x2+5x=n，
方程兩邊同時加上一次項系數一半的平方,得到x2+5x+(
)2=n+()2，
配方得(x+)2=n+()2，
所以，根據題意，得
p=,n+()2=9,則n=
.
所以,由方程x25x+n=1得到
x25x=1
把常數項移到等號的右邊,得到x25x=1+，
方程兩邊同時加上一次項系數一半的平方,得到x25x+()2=1++()2
配方得(x)2=8.即(xp)2=8
故答案選B.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】如圖，△ABC和△ADE均為等腰直角三角形，∠BAC＝∠DAE＝90°，F為EC的中點，連接AF．寫出AF與BD的數量關系和位置關系，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在數學活動課上,老師提出這樣一個問題：“已知
，同學們只用一塊三角板可以畫出它的角平分線嗎？”聰明的小陽經過思考設計了如下方案（如圖）：
（1）在角的兩邊OM、ON上分別取OA=OB；
（2）過點A作DA⊥OM于點A，交ON于點D；過點B作EB⊥ON于點B，交OM于點E，AD、BE交于點C；
（3）作射線OC.
小陽接著解釋說：“此時，△OAC≌△OBC，所以射線OC為∠MON的平分線。”小陽的方案中,△OAC≌△OBC的依據是（ ）
A.SASB.ASAC.HLD.AAS
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠A＝90°，∠ACB＝30°，AC＝10，CD是角平分線．
（1）如圖1，若E是AC邊上的一個定點，在CD上找一點P，使PA+PE的值最小；
（2）如圖2，若E是AC邊上的一個動點，在CD上找一點P，使PA+PE的值最小，并直接寫出其最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠BAC=90°，AB=3，M為邊BC上的點，連接AM．如果將△ABM沿直線AM翻折后，點B恰好落在邊AC的中點處，那么點M到AC的距離是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，
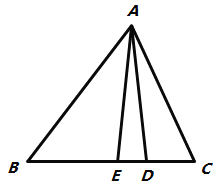
（1）若AE平分∠BAC，AD⊥BC于點D，∠C=74°，∠B=46°，求∠DAE的度數.
（2）若AE是△ABC的中線，BC=4,△ABE的面積為4，EC=3DE，求△ABC面積和△ADE的面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，用同樣規格的規格黑白兩色正方形瓷磚鋪設矩形地面，請觀察圖形并解答有關問題．
在第
個圖中，每一橫行共有________塊瓷磚，每豎行共有________塊瓷磚（均用含的代數式表示）
設鋪設地面所用的瓷磚總塊數
，寫出與的函數關系式（不寫的取值范圍）
按上述鋪設方案，鋪一塊這樣的地面共用了
塊瓷磚，求此時的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在長方形
中，
=4， 
=8，點
是邊上一點，且
，點
是邊
上一動點，連接
，
，則下列結論：① 
；②當
時，平分 
； ③△
周長的最小值為15 ；④當
時，
平分
.其中正確的個數有（ ）
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1是一個長為2m、寬為2n的長方形，沿圖中虛線用剪刀平均分成4個小長方形，然后按圖2的形狀拼成一個正方形．
(1)圖2中陰影部分的面積請用兩種方法表示：① ；②_________.
(2)觀察圖2，請你寫出式子(m＋n)2，(m－n)2，mn之間的等量關系： ；
(3)若x＋y＝－6，xy＝2.75，求x－y的值.
(4)觀察圖3，你能得到怎樣的代數恒等式？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com