
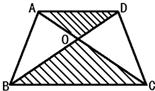
 如圖,已知梯形ABCD中AD=
如圖,已知梯形ABCD中AD= BC,三角形AOD的面積比三角形BOC的面積少12平方厘米,梯形ABCD的面積________.
BC,三角形AOD的面積比三角形BOC的面積少12平方厘米,梯形ABCD的面積________. BC,這一條件可知三角形ABD的面積與三角形BDC的面積比,列出方程即可解答.
BC,這一條件可知三角形ABD的面積與三角形BDC的面積比,列出方程即可解答. BC,所以三角形ABD的面積:三角形BDC的面積=2:5,
BC,所以三角形ABD的面積:三角形BDC的面積=2:5,

 小學課堂作業(yè)系列答案
小學課堂作業(yè)系列答案 金博士一點全通系列答案
金博士一點全通系列答案湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com