
分析 解答此題可設原來長、寬、高分別為a、b、h,那么現在就分別為3a、3b、3h,分別表示出原來的棱長總和、表面積與現在的表面積,即可得出答案.
解答 解:設原來長為a,寬為b,高為h,則現在的長為3a,寬為3b,高為3h;
原來的棱長總和:4(a+b+h)
現在的棱長總和:4(3a+3b+3h)=12(a+b+h)
[12(a+b+h)]÷[4(a+b+h)]=3
原來的表面積;2(ab+ac+bc)
現在的表面積:2(9ab+9ac+9bc)=18(ab+ac+bc)
[18(ab+ac+bc)]÷[2(ab+ac+bc)]=9
答:它的棱長總和擴大3倍,表面積擴大9倍,體積擴大27倍.
故選:A;C.
點評 此題主要考查長方體的表面積和體積計算公式,通過計算可得出規律:長方體的長、寬、高分別擴大3倍,那么棱長總和擴大3倍,表面積就擴大32倍.


科目:小學數學 來源: 題型:解答題
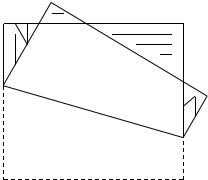 桌子上有一張長方形的紙片,如下圖折疊后,得到的圖開所覆蓋桌面的面積占原長方形面積的$\frac{3}{5}$.已知陰影部分面積為6平方厘米,那么,原長方形面積是多少平方厘米?
桌子上有一張長方形的紙片,如下圖折疊后,得到的圖開所覆蓋桌面的面積占原長方形面積的$\frac{3}{5}$.已知陰影部分面積為6平方厘米,那么,原長方形面積是多少平方厘米?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com