
題目列表(包括答案和解析)
設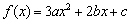 ,若
,若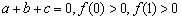 ,求證:
,求證:
(1)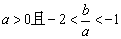 ;
;
(2)方程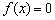 在(0,1)內有兩個實根.
在(0,1)內有兩個實根.
求證:(1)平行六面體的各對角線交于一點,并且在這一點互相平分.
(2)對角線相等的平行六面體是長方體.
已知:平行六面體ABCD-A1B1C1D1

求證:(1)對角線AC1、BD1、CA1、DB1相交于一點,且在這點互相平分;
(2)若AC1=BD1=CA1=DB1時,該平行六面體為長方體.
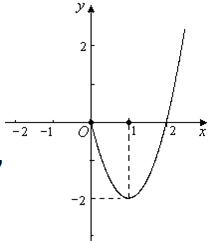 若函數f(x)為奇函數,當x≥0時,f(x)=2x2-4x(如圖).
若函數f(x)為奇函數,當x≥0時,f(x)=2x2-4x(如圖).| a•2x-2 |
| 1+2x |
| 1 |
| 2 |
一:填空題
1、2; 2、 x∈R,使x2+1<x; 3、π; 4、;
5、既不充分也不必要條件;
x∈R,使x2+1<x; 3、π; 4、;
5、既不充分也不必要條件;
6、1+i; 7、; 8、5; 9、; 10、(-∞, -)∪(,+∞);
11、2或5; 12、9; 13、b1?b22?b33?…?bnn=; 14、;
二: 解答題
解答題
15.解:(1)∵(a=(cosα,sinα) (b=(cosβ,sinβ)
∴(a?(b=cos(α-β) =cos= …………………………………………5分
(2)∵ ∴
∴ ………7分
………7分
 α+β=2α-(α-β)= -(α-β)
……………………………………9分
α+β=2α-(α-β)= -(α-β)
……………………………………9分
∴

 或
或
 或7……………14分
或7……………14分
16、證明:(1)令BC中點為N,BD中點為M,連結MN、EN
∵MN是△ABC的中位線
 ∴ MN∥CD …………………………2分
∴ MN∥CD …………………………2分
由條件知AE∥CD ∴MN∥AE 又MN=CD=AE
∴四邊形AEMN為平行四邊形
∴AN∥EM …………………………4分
∵AN 面BED, EM
面BED, EM 面BED
面BED
∴AN∥面BED……………………6分
 (2)
(2) ∵AE⊥面ABC, AN
∵AE⊥面ABC, AN 面ABC
面ABC
∴AE⊥AN 又∵AE∥CD,AN∥EM∴EM⊥CD………………8分
∵N為BC中點,AB=AC∴AN⊥BC
 ∴EM⊥BC………………………………………………10分
∴EM⊥BC………………………………………………10分
∴EM⊥面BCD…………………………………………12分
∵EM 面BED ∴ 面BED⊥面BCD ……14分
面BED ∴ 面BED⊥面BCD ……14分
17.解:(1)取弦的中點為M,連結OM
由平面幾何知識,OM=1
 …………………………………………3分
…………………………………………3分
解得: ,
, ………………………………………5分
………………………………………5分
∵直線過F、B ,∴ 則
則 …………………………………………7分
…………………………………………7分
(2)設弦的中點為M,連結OM
則
 ……………………………………10分
……………………………………10分
解得 …………………………………………12分
…………………………………………12分
 ∴
∴ ……………………………15分
……………………………15分
18.(1)延長BD、CE交于A,則AD= ,AE=2
,AE=2
則S△ADE= S△BDE= S△BCE= , ∵S△APQ=
, ∵S△APQ= ,
,
∴ ∴
∴
 …………………7分
…………………7分
(2)

= ?
? ………………12分
………………12分
當 ,即
,即
 ……15分
……15分
19.解(1)證:
 由
由 得
得
在C1上點 處的切線為y-2e=2(x-e),即y=2x
處的切線為y-2e=2(x-e),即y=2x
又在C2上點 處切線可計算得y-2e=2(x-e),即y=2x
處切線可計算得y-2e=2(x-e),即y=2x
∴直線l與C1、C2都相切,且切于同一點(e,2e) …………………5分
(2)據題意:M(t, +e),N(t,2elnt),P(t,2t)
∵+e-2t=≥0,∴+e ≥2t
設h(t)= 2t-2elnt,則由h/(t)=2-=0得t=e ;
當t∈(0,e)時h/(t)<0,h(t)單調遞減;且當t∈(e,+∞)時h/(t)>0,h(t)單調遞增;
∴t>0有h(t)≥h(e)=0 ∴2t≥2elnt
∴f(t)=+e-2t-(2t-2elnt)= +e -4t+2elnt………………4分
f(t)= +2e-4==≥0…………………7分
∴ 在
在 上遞增∴當
上遞增∴當 時
時 ………10分
………10分
(3)
設上式為 ,假設
,假設 取正實數,則
取正實數,則 ?
?
當 時,
時, ,
, 遞減;
遞減;
當 ,
, ,
, 遞增. ……………………………………12分
遞增. ……………………………………12分
∵


∴不存在正整數 ,使得
,使得 即
即 …………………16分
…………………16分
20.解:(1) ,
,
 ,
, 對一切
對一切 恒成立
恒成立
 的最小值,又
的最小值,又 ,
,
 ………………4分
………………4分
(2) 這5個數中成等比且公比
這5個數中成等比且公比 的三數只能為
的三數只能為
 只能是
只能是 ,
,
 …………………………8分
…………………………8分


 ,
, ,
,
 ,
, 顯然成立
……………………………………12分
顯然成立
……………………………………12分
當 時,
時, ,
,

∴ ∴使
∴使 成立的自然數n恰有4個正整數的p值為3……16分
成立的自然數n恰有4個正整數的p值為3……16分
三:理科附加題
21. A.解:(1)
∴ ∴AB=CD
…………………………4分
∴AB=CD
…………………………4分
(2)由相交弦定理得2×1=(3+OP)(3-OP)
∴ ,∴
,∴ ……………………………………10分
……………………………………10分
B.解:依題設有: ………………………………………4分
………………………………………4分
令 ,則
,則 …………………………………………5分
…………………………………………5分
 …………………………………………7分
…………………………………………7分




 ………………………………10分
………………………………10分
C.解:以有點為原點,極軸為 軸正半軸,建立平面直角坐標系,兩坐標系中取相同的長度單位.(1)
軸正半軸,建立平面直角坐標系,兩坐標系中取相同的長度單位.(1) ,
, ,由
,由 得
得 .
.
所以 .
.
即 為圓
為圓 的直角坐標方程. ……………………………………3分
的直角坐標方程. ……………………………………3分
同理 為圓
為圓 的直角坐標方程. ……………………………………6分
的直角坐標方程. ……………………………………6分
(2)由
相減得過交點的直線的直角坐標方程為 . …………………………10分
. …………………………10分
D.證明:(1)因為
所以 …………………………………………4分
…………………………………………4分
(2)∵ …………………………………………6分
…………………………………………6分
同理, ,
, ……………………………………8分
……………………………………8分
三式相加即得 ……………………………10分
……………………………10分
22.解:(1)記“恰好選到1個曾參加過數學研究性學習活動的同學”為事件的 ,
,
則其概率為 …………………………………………4分
…………………………………………4分
答:恰好選到1個曾經參加過數學研究性學習活動的同學的概率為
(2)隨機變量
P(ξ=2)= =; P(ξ=3)= =; ………7分
………7分

2
3
4
P



∴隨機變量 的分布列為
的分布列為
 ………………10分
………………10分
23.(1) ,
, ,
, ,
,
 ,
, ,
, ………………3分
………………3分
(2)平面BDD1的一個法向量為 ,設平面BFC1的法向量為
,設平面BFC1的法向量為
 ∴
∴
取 得平面BFC1的一個法向量
得平面BFC1的一個法向量

∴所求的余弦值為 ……………………………………6分
……………………………………6分
(3)設 (
( )
)
 ,由
,由 得
得
即 ,
,


 ,
, 當
當 時,
時, 當
當 時,∴
時,∴ ……………10分
……………10分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com