
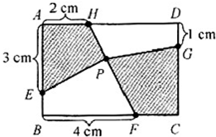
 如圖,有一個寬4厘米、長6厘米的長方形ABCD,在各個邊上取點E、F、G、H,在連接H、F的線上取點P,連接EP和GP.當四邊形AEPH的面積是5平方厘米時,求四邊形PFCG的面積.
如圖,有一個寬4厘米、長6厘米的長方形ABCD,在各個邊上取點E、F、G、H,在連接H、F的線上取點P,連接EP和GP.當四邊形AEPH的面積是5平方厘米時,求四邊形PFCG的面積. =12(平方厘米),
=12(平方厘米), 1×6,
1×6, 4×4,
4×4,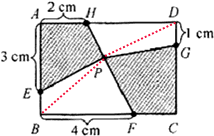


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:小學數學 來源: 題型:
 如圖,有一個長6厘米,寬4厘米的長方形ABCD,已知線段DG、AH、AE、BF的長度依次是1,2,3,4厘米,且四邊形AEPH的面積是5平方厘米,且四邊形PFCG的面積是多少平方厘米?
如圖,有一個長6厘米,寬4厘米的長方形ABCD,已知線段DG、AH、AE、BF的長度依次是1,2,3,4厘米,且四邊形AEPH的面積是5平方厘米,且四邊形PFCG的面積是多少平方厘米?查看答案和解析>>
科目:小學數學 來源: 題型:
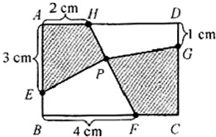 如圖,有一個寬4厘米、長6厘米的長方形ABCD,在各個邊上取點E、F、G、H,在連接H、F的線上取點P,連接EP和GP.當四邊形AEPH的面積是5平方厘米時,求四邊形PFCG的面積.
如圖,有一個寬4厘米、長6厘米的長方形ABCD,在各個邊上取點E、F、G、H,在連接H、F的線上取點P,連接EP和GP.當四邊形AEPH的面積是5平方厘米時,求四邊形PFCG的面積.查看答案和解析>>
科目:小學數學 來源: 題型:
 (2009?西藏)如圖,有一個長20厘米,寬15厘米的長方形硬紙,從四個角各剪去一個邊長4厘米的正方形后,做成一個無蓋的長方體.
(2009?西藏)如圖,有一個長20厘米,寬15厘米的長方形硬紙,從四個角各剪去一個邊長4厘米的正方形后,做成一個無蓋的長方體.查看答案和解析>>
科目:小學數學 來源:西藏 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com