
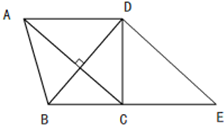
 在等腰梯形ABCD中,延長BC到E點,已知線段AC與BD互相垂直,AC與DE互相平行,AD=CE,AD+BC=10厘米,求三角形BDE的面積.
在等腰梯形ABCD中,延長BC到E點,已知線段AC與BD互相垂直,AC與DE互相平行,AD=CE,AD+BC=10厘米,求三角形BDE的面積. ×10=5(厘米),
×10=5(厘米),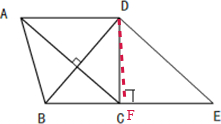


科目:小學數學 來源: 題型:
 如圖,在等腰梯形ABCD中,上底AD=20厘米,下底BC=100厘米,高為40厘米,另有一條邊長為40厘米的正方形CEFG沿直線L以每分鐘10厘米的速度向左勻速平移(邊CE始終在直線L上)當正方形運動到第10分鐘時,在圖中畫出正方形的位置,用陰影表示等腰梯形與正方形的重疊部分,并求出陰影部分的面積.
如圖,在等腰梯形ABCD中,上底AD=20厘米,下底BC=100厘米,高為40厘米,另有一條邊長為40厘米的正方形CEFG沿直線L以每分鐘10厘米的速度向左勻速平移(邊CE始終在直線L上)當正方形運動到第10分鐘時,在圖中畫出正方形的位置,用陰影表示等腰梯形與正方形的重疊部分,并求出陰影部分的面積.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com