
分析 鈍角三角形中最大角的度數大于90°,由三角形的內角和是180°可以得到:另外兩個內角的和應小于90°,因此這兩個內角一定有一個角小于45°,從而問題得解.
解答 解:因為鈍角三角形中最大角的度數大于90°,
則另外兩個內角的和應小于90°,
依據數量間的和差關系得:
這兩個內角一定有一個角小于90°÷2=45°.
故答案為:√.
點評 解答此題的關鍵是:利用已知條件及三角形的內角和定理得出另外兩個內角的和應小于90°,再據數量間的和差關系得到這兩個內角一定有一個角小于45°.


科目:小學數學 來源: 題型:計算題
| 452+98= | 1.25×8= | 640÷16= | $\frac{1}{5}$×$\frac{1}{2}$÷$\frac{1}{5}$×$\frac{1}{2}$= | 45÷1.25÷8= |
| 5.01-1.8= | 0.25×0.4= | 0.88+0.12= | 6.5+9.5+3.5= | ($\frac{3}{8}$-0.375)×5= |
查看答案和解析>>
科目:小學數學 來源: 題型:操作題
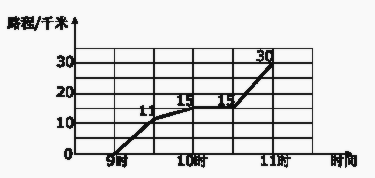
查看答案和解析>>
科目:小學數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com