
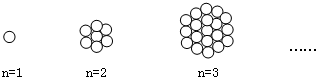 如圖,當n=1時,圖中有1個圓;當n=2時,圖中有7個圓;當n=3時,圖中有19個圓;…,按此規律,當n=5時,圖中有________個圓.
如圖,當n=1時,圖中有1個圓;當n=2時,圖中有7個圓;當n=3時,圖中有19個圓;…,按此規律,當n=5時,圖中有________個圓.

科目:小學數學 來源: 題型:
 如圖,一只螞蚱站在1號位置上,第1次跳1步,站在2號位置上;第2次跳2步,站在4號位置上;第3次跳3步,站在1號位置上…第n次跳n步.當螞蚱沿順時針方向跳100次時,到達
如圖,一只螞蚱站在1號位置上,第1次跳1步,站在2號位置上;第2次跳2步,站在4號位置上;第3次跳3步,站在1號位置上…第n次跳n步.當螞蚱沿順時針方向跳100次時,到達查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com