把一個橫截面是正方形的長方體木料切削成一個最大的圓柱,此圓柱的表面積是32.97平方厘米,底面直徑與高的比是1:3,原長方體的表面積是多少平方厘米?
解:設長方體的橫截面的邊長為x厘米,則長方體的高為3x厘米,則最大圓柱的底面直徑是x厘米,高是3x厘米,所以:
3.14×
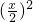
×2+3.14x×3x=32.97,
1.57x
2+9.42x
2=32.97,
10.99x
2=32.97,
x
2=3;
則長方體的表面積為:(3x×x+3x×x+x×x)×2,
=(3x
2+3x
2+x
2)×2,
=7x
2×2,
=14x
2,
=14×3,
=42(平方厘米);
答:這個長方體的表面積是42平方厘米.
分析:長方體木料切削成一個最大的圓柱,則這個圓柱的底面直徑等于橫截面的邊長,圓柱的高等于長方體的高,由此設長方體的橫截面的邊長為x厘米,則長方體的高為3x厘米,根據圓柱的表面積公式可得關于x的方程,求得x的值再利用長方體的表面積公式解答.
點評:抓住長方體內最大的圓柱的特點即可解答,此題中求出x
2為等量代換的值是解決問題的關鍵.

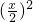 ×2+3.14x×3x=32.97,
×2+3.14x×3x=32.97,
