Question

（2010?永泰縣）先填表，再作答．
（1）完成表格中未填的部分．
（2）多邊形內角和與它的邊數關系是：

（n-2）?180°

（3）一個八邊形的內角和是

1080

度．

Answer 1

分析：根據過同一頂點作出的對角線把多邊形分成的三角形的個數的規律，再利用三角形的內角和等于180°即可推出多邊形的內角和公式．

解答：解：（1）n邊形的內角和等于（n-2）?180°，
理由如下：三角形內角和    四邊形內角和    五邊形內角和    六邊形內角和
              180°×1       180°×2         180°×3        180°×4
據此填表如下：


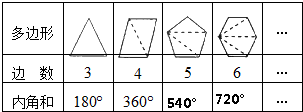
（2）由上述推理計算可得：過n邊形某一頂點可畫（n-3）條對角線，把n邊形分為（n-2）個三角形，
這（n-2）個三角形的內角和之和就等于n邊形的內角和，即多邊形內角和是：（n-2）?180°．
答：多邊形內角和是：（n-2）?180°．

（3）當n=8時，（n-2）?180°=1080°，
答：八邊形的內角和是1080°．
故答案為：（n-2）?180°；1080．

點評：本題考查了多邊形的內角和公式的推導，理清過同一個頂點把多邊形分成的三角形的個數是解題的關鍵，也是本題的難點．