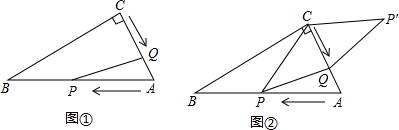
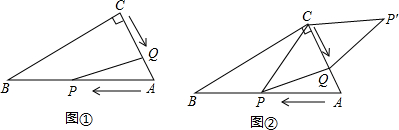
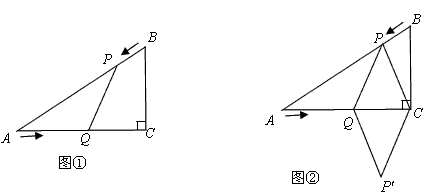
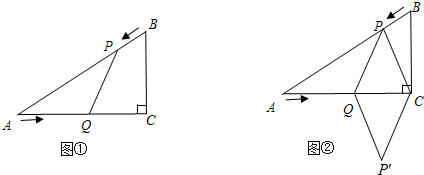
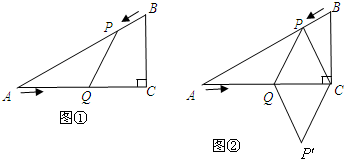
已知,如圖①,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,點P從點A沿AB以每秒2cm的速度向點B運動,點Q從點C以每秒1cm的速度向點A運動,設點P、Q分別從點A、C同時出發,運動時間為t(秒)(0<t<6),回答下列問題:
(1)直接寫出線段AP、AQ的長(含t的代數式表示):AP=
2t
2t
,AQ=
6-t
6-t
;
(2)設△APQ 的面積為S,寫出S與t的函數關系式;
(3)如圖②,連接PC,并把△PQC沿QC翻折,得到四邊形PQP′C,那么是否存在某一時間t,使四邊形PQP′C為菱形?若存在,求出此時t的值;若不存在,說明理由.