
題目列表(包括答案和解析)
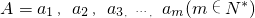 ,且對任意的b∈M,存在ai,aj∈A(1≤i≤j≤m),使得b=λ1ai+λ2aj(其中λ1,λ2∈{-1,0,1}),則稱集合A為集合M的一個m元基底.
,且對任意的b∈M,存在ai,aj∈A(1≤i≤j≤m),使得b=λ1ai+λ2aj(其中λ1,λ2∈{-1,0,1}),則稱集合A為集合M的一個m元基底. ,且對任意的b∈M,存在ai,aj∈A(1≤i≤j≤m),使得b=λ1ai+λ2aj(其中λ1,λ2∈{﹣1,0,1}),則稱集合A為集合M的一個m元基底.
,且對任意的b∈M,存在ai,aj∈A(1≤i≤j≤m),使得b=λ1ai+λ2aj(其中λ1,λ2∈{﹣1,0,1}),則稱集合A為集合M的一個m元基底.湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com