
題目列表(包括答案和解析)
若數列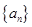 的前
的前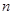 項和為
項和為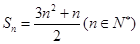 :;
:;
(Ⅰ) 求數列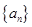 的通項公式
的通項公式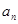 ;
;
(Ⅱ) 設數列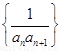 的前
的前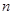 項和為
項和為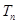 ,是否存在實數
,是否存在實數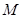 ,使得
,使得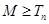 對一切正整數都成立?若存在,求出
對一切正整數都成立?若存在,求出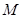 的最小值,若不存在,請說明理由.
的最小值,若不存在,請說明理由.
(12分)已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() (
(![]() 為正整數)
為正整數)
(I)求數列![]() 的通項公式;
的通項公式;
已知數列 的前
的前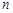 項和為
項和為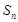 ,且
,且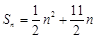 。數列
。數列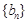 滿足
滿足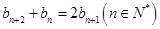 ,
,
且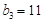 ,
,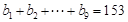 。
。
(1)求數列 ,
,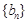 的通項公式;
的通項公式;
(2)設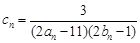 ,數列
,數列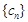 的前
的前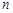 項和為
項和為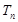 ,求使不等式
,求使不等式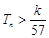 對一切
對一切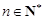 都成立的最大正整數
都成立的最大正整數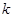 的值;
的值;
(3)設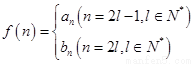 ,是否存在
,是否存在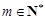 ,使得
,使得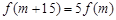 成立?若存在,求出
成立?若存在,求出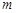 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
已知數列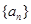 的前
的前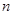 項和為
項和為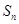 ,點
,點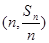 在直線
在直線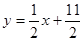 上.數列
上.數列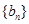 滿足
滿足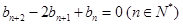 ,且
,且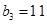 ,前9項和為153.
,前9項和為153.
(1)求數列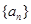 、
、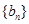 {的通項公式;
{的通項公式;
(2)設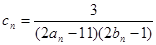 ,數列
,數列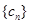 的前
的前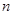 和為
和為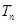 ,求使不等式
,求使不等式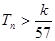 對一切
對一切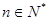 都成立的最大正整數
都成立的最大正整數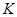 的值;
的值;
(3)設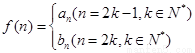 ,問是否存在
,問是否存在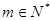 ,使得
,使得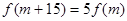 成立?若存在,求出
成立?若存在,求出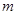 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
已知數列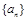 的前
的前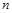 項和
項和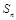 和通項
和通項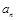 滿足
滿足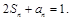 數列
數列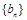 中,
中,

(1)求數列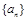 ,
,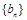 的通項公式;
的通項公式;
(2)數列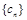 滿足
滿足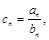 是否存在正整數
是否存在正整數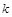 ,使得
,使得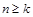 時
時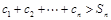 恒成立?若存在,求
恒成立?若存在,求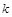 的最小值;若不存在,試說明理由.
的最小值;若不存在,試說明理由.
一、選擇題(本大題共8小題,每小題5分,共40分)
1.A 2.D 3.D 4.C 5.C 6.B 7.C 8.A
二、填空題(本大題共6小題,每小題5分,共30分)
9.數學理科.files/image273.gif) 10.60 11.
10.60 11.數學理科.files/image275.gif)
12.(1) (2)
13.1, 數學理科.files/image277.gif) 14.
14.數學理科.files/image279.gif) ,
,數學理科.files/image281.gif)
注:兩個空的填空題第一個空填對得2分,第二個空填對得3分.
三、解答題(本大題共6小題,共80分)
15.(本小題滿分13分)
解:(Ⅰ)設等比數列數學理科.files/image074.gif) 的公比為
的公比為數學理科.files/image284.gif) ,依題意有
,依題意有數學理科.files/image286.gif) , (1)
, (1)
又數學理科.files/image150.gif) ,將(1)代入得
,將(1)代入得數學理科.files/image289.gif) .所以
.所以數學理科.files/image291.gif) .
.
于是有數學理科.files/image293.gif) ………………3分
………………3分
解得數學理科.files/image295.gif) 或
或數學理科.files/image297.gif) ………………6分
………………6分
又數學理科.files/image074.gif) 是遞增的,故
是遞增的,故數學理科.files/image299.gif) .
………………7分
.
………………7分
所以數學理科.files/image301.gif) .
………………8分
.
………………8分
(Ⅱ)數學理科.files/image303.gif) ,
,數學理科.files/image305.gif) .
………………10分
.
………………10分
故由題意可得數學理科.files/image307.gif) ,解得
,解得數學理科.files/image309.gif) 或
或數學理科.files/image311.gif) .又
.又數學理科.files/image313.gif) , …………….12分
, …………….12分
所以滿足條件的數學理科.files/image060.gif) 的最小值為13.
………………13分
的最小值為13.
………………13分
16. (本小題滿分13分)
解:(Ⅰ)由數學理科.files/image316.gif) 且
且數學理科.files/image318.gif) ,
,
所以數學理科.files/image320.gif) .
…………………4分
.
…………………4分
于是數學理科.files/image322.gif) . …………7分
. …………7分
(Ⅱ)由正弦定理可得數學理科.files/image324.gif) ,
,
所以數學理科.files/image326.gif) .
…………………….10分
.
…………………….10分
由數學理科.files/image173.gif) 得
得數學理科.files/image329.gif) .
………………11分
.
………………11分
即數學理科.files/image331.gif) ,
,
解得數學理科.files/image333.gif) .即
.即數學理科.files/image175.gif) =7 .
…………13分
=7 .
…………13分
數學理科.files/image335.gif) 17.(本小題滿分14分)
17.(本小題滿分14分)
解法一:(Ⅰ)∵正方形數學理科.files/image337.gif) ,∴
,∴數學理科.files/image339.gif)
又二面角數學理科.files/image341.gif) 是直二面角,
是直二面角,
∴數學理科.files/image343.gif) ⊥平面
⊥平面數學理科.files/image182.gif) .
.
∵數學理科.files/image346.gif)
數學理科.files/image348.gif) 平面
平面數學理科.files/image182.gif) ,
,
∴數學理科.files/image343.gif) ⊥
⊥數學理科.files/image346.gif) .
.
又數學理科.files/image353.gif) ,
,數學理科.files/image355.gif) ,
,數學理科.files/image182.gif) 是矩形,
是矩形,數學理科.files/image188.gif) 是
是數學理科.files/image190.gif) 的中點,
的中點,
∴數學理科.files/image360.gif) =
=數學理科.files/image362.gif) ,
,數學理科.files/image364.gif) ,
,數學理科.files/image366.gif) =
=數學理科.files/image368.gif) ,
,
∴數學理科.files/image346.gif) ⊥
⊥數學理科.files/image371.gif) 又
又數學理科.files/image343.gif)
數學理科.files/image374.gif) =
=數學理科.files/image376.gif) ,
,
∴數學理科.files/image346.gif) ⊥平面
⊥平面數學理科.files/image379.gif) ,
,
而數學理科.files/image346.gif)
數學理科.files/image348.gif) 平面
平面數學理科.files/image382.gif) ,故平面
,故平面數學理科.files/image382.gif) ⊥平面
⊥平面數學理科.files/image385.gif) ……………………5分
……………………5分
(Ⅱ)如圖,由(Ⅰ)知平面數學理科.files/image382.gif) ⊥平面
⊥平面數學理科.files/image388.gif) ,且交于
,且交于數學理科.files/image390.gif) ,在平面
,在平面數學理科.files/image388.gif) 內作
內作數學理科.files/image393.gif) ⊥
⊥數學理科.files/image390.gif) ,垂足為
,垂足為數學理科.files/image396.gif) ,則
,則數學理科.files/image393.gif) ⊥平面
⊥平面數學理科.files/image382.gif) .
.
∴∠數學理科.files/image400.gif) 是
是數學理科.files/image402.gif) 與平面
與平面數學理科.files/image382.gif) 所成的角.
……………………7分
所成的角.
……………………7分
∴在Rt△數學理科.files/image379.gif) 中,
中,數學理科.files/image402.gif) =
=數學理科.files/image407.gif) .
.
數學理科.files/image409.gif) .
.
即數學理科.files/image402.gif) 與平面
與平面數學理科.files/image382.gif) 所成的角為
所成的角為數學理科.files/image411.gif) .
………………………9分
.
………………………9分
(Ⅲ)由(Ⅱ),數學理科.files/image393.gif) ⊥平面
⊥平面數學理科.files/image382.gif) .作
.作數學理科.files/image415.gif) ⊥
⊥數學理科.files/image417.gif) ,垂足為
,垂足為數學理科.files/image419.gif) ,連結
,連結數學理科.files/image421.gif) ,則
,則數學理科.files/image421.gif) ⊥
⊥數學理科.files/image417.gif) ,
,
∴∠數學理科.files/image425.gif) 為二面角
為二面角數學理科.files/image427.gif) 的平面角. ……………………….11分
的平面角. ……………………….11分
∵在Rt△數學理科.files/image165.gif) 中,
中,數學理科.files/image415.gif) =
=數學理科.files/image431.gif)
數學理科.files/image180.gif) ,在Rt△
,在Rt△數學理科.files/image379.gif) 中,
中,數學理科.files/image435.gif) .
.
∴在Rt△數學理科.files/image425.gif) 中,
中,數學理科.files/image438.gif) ………13分
………13分
即二面角數學理科.files/image427.gif) 的大小為arcsin
的大小為arcsin數學理科.files/image441.gif) .
………………………………14分
.
………………………………14分
數學理科.files/image442.gif) 解法二:
解法二:
如圖,以數學理科.files/image444.gif) 為原點建立直角坐標系
為原點建立直角坐標系數學理科.files/image446.gif) ,
,
則數學理科.files/image444.gif) (0,0,0),
(0,0,0),數學理科.files/image376.gif) (0,2
(0,2數學理科.files/image180.gif) ,0),
,0),
數學理科.files/image223.gif) (0,2
(0,2數學理科.files/image180.gif) ,2
,2數學理科.files/image180.gif) ),
),數學理科.files/image188.gif) (
(數學理科.files/image180.gif) ,
,數學理科.files/image180.gif) ,0),
,0),
數學理科.files/image457.gif) (
(數學理科.files/image180.gif) ,0,0).
,0,0).
(Ⅰ)數學理科.files/image460.gif) =(
=(數學理科.files/image180.gif) ,
,數學理科.files/image180.gif) ,0),
,0),數學理科.files/image464.gif) =(
=(數學理科.files/image180.gif) ,
,數學理科.files/image467.gif) ,0),
,0),
數學理科.files/image469.gif) =(0,0,2
=(0,0,2數學理科.files/image180.gif) ),
),
∴數學理科.files/image460.gif) ?
?數學理科.files/image464.gif) =(
=(數學理科.files/image180.gif) ,
,數學理科.files/image180.gif) ,0)?(
,0)?(數學理科.files/image180.gif) ,
,數學理科.files/image467.gif) ,0)=0,
,0)=0,
數學理科.files/image460.gif) ?
?數學理科.files/image469.gif) =(
=(數學理科.files/image180.gif) ,
,數學理科.files/image180.gif) ,0)?(0,0,2
,0)?(0,0,2數學理科.files/image180.gif) )= 0.
)= 0.
∴數學理科.files/image346.gif) ⊥
⊥數學理科.files/image402.gif) ,
,數學理科.files/image346.gif) ⊥
⊥數學理科.files/image476.gif) ,
,
∴數學理科.files/image346.gif) ⊥平面
⊥平面數學理科.files/image479.gif) ,又
,又數學理科.files/image346.gif)
數學理科.files/image348.gif) 平面
平面數學理科.files/image482.gif) ,故平面
,故平面數學理科.files/image482.gif) ⊥平面
⊥平面數學理科.files/image479.gif) . ……5分
. ……5分
(Ⅱ)設數學理科.files/image196.gif) 與平面
與平面數學理科.files/image382.gif) 所成角為
所成角為數學理科.files/image488.gif) .
.
由題意可得數學理科.files/image460.gif) =(
=(數學理科.files/image180.gif) ,
,數學理科.files/image180.gif) ,0),
,0),數學理科.files/image492.gif) =(0,2
=(0,2數學理科.files/image180.gif) ,2
,2 數學理科.files/image180.gif) ),
),數學理科.files/image464.gif) =(
=(數學理科.files/image180.gif) ,
,數學理科.files/image467.gif) ,0).
,0).
設平面數學理科.files/image382.gif) 的一個法向量為
的一個法向量為數學理科.files/image499.gif) =(
=(數學理科.files/image020.gif) ,
,數學理科.files/image089.gif) ,1),
,1),
由數學理科.files/image503.gif) .
.
數學理科.files/image505.gif) .
.
∴數學理科.files/image196.gif) 與平面
與平面數學理科.files/image382.gif) 所成角的大小為
所成角的大小為數學理科.files/image508.gif) .
……………..9分
.
……………..9分
(Ⅲ)因數學理科.files/image499.gif) =(1,-1,1)是平面
=(1,-1,1)是平面數學理科.files/image382.gif) 的一個法向量,
的一個法向量,
又數學理科.files/image512.gif) ⊥平面
⊥平面數學理科.files/image337.gif) ,平面
,平面數學理科.files/image337.gif) 的一個法向量
的一個法向量數學理科.files/image516.gif) =(
=(數學理科.files/image180.gif) ,0,0),
,0,0),
∴設數學理科.files/image499.gif) 與
與數學理科.files/image516.gif) 的夾角為
的夾角為數學理科.files/image519.gif) ,得
,得數學理科.files/image521.gif) ,
,
∴二面角數學理科.files/image427.gif) 的大小為
的大小為數學理科.files/image524.gif)
數學理科.files/image526.gif) . ………………………………14分
. ………………………………14分
18. (本小題滿分13分)
解:(Ⅰ)設事件數學理科.files/image444.gif) 表示甲運動員射擊一次,恰好擊中9環以上(含9環),則
表示甲運動員射擊一次,恰好擊中9環以上(含9環),則
數學理科.files/image529.gif) .
……………….3分
.
……………….3分
甲運動員射擊3次均未擊中9環以上的概率為
數學理科.files/image531.gif) .
…………………5分
.
…………………5分
所以甲運動員射擊3次,至少有1次擊中9環以上的概率為
數學理科.files/image533.gif) .
………………6分
.
………………6分
(Ⅱ)記乙運動員射擊1次,擊中9環以上為事件數學理科.files/image376.gif) ,則
,則
數學理科.files/image536.gif) …………………8分
…………………8分
由已知數學理科.files/image202.gif) 的可能取值是0,1,2.
…………………9分
的可能取值是0,1,2.
…………………9分
數學理科.files/image539.gif) ;
;
數學理科.files/image541.gif) ;
;
數學理科.files/image543.gif) .
.
數學理科.files/image202.gif) 的分布列為
的分布列為
數學理科.files/image202.gif)
0
1
2
數學理科.files/image022.gif)
0.05
0.35
0.6
………………………12分
所以數學理科.files/image548.gif)
故所求數學期望為數學理科.files/image550.gif) .
………………………13分
.
………………………13分
19. (本小題滿分14分)
解:(Ⅰ)由已知數學理科.files/image552.gif) ,故
,故數學理科.files/image554.gif) ,所以直線
,所以直線數學理科.files/image219.gif) 的方程為
的方程為數學理科.files/image557.gif) .
.
將圓心數學理科.files/image223.gif)
數學理科.files/image560.gif) 代入方程易知
代入方程易知數學理科.files/image219.gif) 過圓心
過圓心數學理科.files/image223.gif) . …………………………3分
. …………………………3分
(Ⅱ) 當直線數學理科.files/image219.gif) 與
與數學理科.files/image020.gif) 軸垂直時,易知
軸垂直時,易知數學理科.files/image566.gif) 符合題意; ………………4分
符合題意; ………………4分
當直線與數學理科.files/image020.gif) 軸不垂直時,設直線
軸不垂直時,設直線數學理科.files/image219.gif) 的方程為
的方程為數學理科.files/image570.gif) ,由于
,由于數學理科.files/image572.gif) ,
,
所以數學理科.files/image574.gif) 由
由數學理科.files/image576.gif) ,解得
,解得數學理科.files/image578.gif) .
.
故直線數學理科.files/image219.gif) 的方程為
的方程為數學理科.files/image566.gif) 或
或數學理科.files/image582.gif) . ………………8分
. ………………8分
(Ⅲ)當數學理科.files/image219.gif) 與
與數學理科.files/image020.gif) 軸垂直時,易得
軸垂直時,易得數學理科.files/image586.gif) ,
,數學理科.files/image588.gif) ,又
,又數學理科.files/image217.gif) 則
則數學理科.files/image591.gif)
數學理科.files/image593.gif) ,故
,故數學理科.files/image595.gif) . 即
. 即數學理科.files/image597.gif) .
………………10分
.
………………10分
當數學理科.files/image219.gif) 的斜率存在時,設直線
的斜率存在時,設直線數學理科.files/image219.gif) 的方程為
的方程為數學理科.files/image570.gif) ,代入圓的方程得
,代入圓的方程得
數學理科.files/image602.gif) .則
.則數學理科.files/image604.gif)
數學理科.files/image606.gif) ,即
,即數學理科.files/image608.gif) ,
,
數學理科.files/image610.gif)
數學理科.files/image612.gif) .又由
.又由數學理科.files/image614.gif) 得
得數學理科.files/image616.gif) ,
,
則數學理科.files/image618.gif) .
.
故數學理科.files/image620.gif)
數學理科.files/image622.gif) .
.
綜上,數學理科.files/image243.gif) 的值為定值,且
的值為定值,且數學理科.files/image597.gif) .
…………14分
.
…………14分
另解一:連結數學理科.files/image626.gif) ,延長交
,延長交數學理科.files/image232.gif) 于點
于點數學理科.files/image629.gif) ,由(Ⅰ)知
,由(Ⅰ)知數學理科.files/image631.gif) .又
.又數學理科.files/image633.gif) 于
于數學理科.files/image227.gif) ,
,
故△數學理科.files/image636.gif) ∽△
∽△數學理科.files/image638.gif) .于是有
.于是有數學理科.files/image640.gif) .
.
由數學理科.files/image642.gif) 得
得
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com