
題目列表(包括答案和解析)
已知函數(shù) 的圖象過(guò)坐標(biāo)原點(diǎn)O,且在點(diǎn)
的圖象過(guò)坐標(biāo)原點(diǎn)O,且在點(diǎn) 處的切線的斜率是
處的切線的斜率是 .
.
(Ⅰ)求實(shí)數(shù) 的值;
的值;
(Ⅱ)求 在區(qū)間
在區(qū)間 上的最大值;
上的最大值;
(Ⅲ)對(duì)任意給定的正實(shí)數(shù) ,曲線
,曲線 上是否存在兩點(diǎn)P、Q,使得
上是否存在兩點(diǎn)P、Q,使得 是以O(shè)為直角頂點(diǎn)的直角三角形,且此三角形斜邊中點(diǎn)在
是以O(shè)為直角頂點(diǎn)的直角三角形,且此三角形斜邊中點(diǎn)在 軸上?說(shuō)明理由.
軸上?說(shuō)明理由.
【解析】第一問(wèn)當(dāng) 時(shí),
時(shí), ,則
,則 。
。
依題意得: ,即
,即 解得
解得
第二問(wèn)當(dāng) 時(shí),
時(shí), ,令
,令 得
得 ,結(jié)合導(dǎo)數(shù)和函數(shù)之間的關(guān)系得到單調(diào)性的判定,得到極值和最值
,結(jié)合導(dǎo)數(shù)和函數(shù)之間的關(guān)系得到單調(diào)性的判定,得到極值和最值
第三問(wèn)假設(shè)曲線 上存在兩點(diǎn)P、Q滿足題設(shè)要求,則點(diǎn)P、Q只能在
上存在兩點(diǎn)P、Q滿足題設(shè)要求,則點(diǎn)P、Q只能在 軸兩側(cè)。
軸兩側(cè)。
不妨設(shè) ,則
,則 ,顯然
,顯然
∵ 是以O(shè)為直角頂點(diǎn)的直角三角形,∴
是以O(shè)為直角頂點(diǎn)的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設(shè)要求的兩點(diǎn)P、Q;
(*)若方程(*)有解,存在滿足題設(shè)要求的兩點(diǎn)P、Q;
若方程(*)無(wú)解,不存在滿足題設(shè)要求的兩點(diǎn)P、Q.
(Ⅰ)當(dāng) 時(shí),
時(shí), ,則
,則 。
。
依題意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①當(dāng) 時(shí),
時(shí), ,令
,令 得
得
當(dāng) 變化時(shí),
變化時(shí), 的變化情況如下表:
的變化情況如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
極小值 |
單調(diào)遞增 |
極大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值為2.
上的最大值為2.
②當(dāng) 時(shí),
時(shí),  .當(dāng)
.當(dāng) 時(shí),
時(shí),  ,
, 最大值為0;
最大值為0;
當(dāng) 時(shí),
時(shí),  在
在 上單調(diào)遞增。∴
上單調(diào)遞增。∴ 在
在 最大值為
最大值為 。
。
綜上,當(dāng) 時(shí),即
時(shí),即 時(shí),
時(shí), 在區(qū)間
在區(qū)間 上的最大值為2;
上的最大值為2;
當(dāng) 時(shí),即
時(shí),即 時(shí),
時(shí), 在區(qū)間
在區(qū)間 上的最大值為
上的最大值為 。
。
(Ⅲ)假設(shè)曲線 上存在兩點(diǎn)P、Q滿足題設(shè)要求,則點(diǎn)P、Q只能在
上存在兩點(diǎn)P、Q滿足題設(shè)要求,則點(diǎn)P、Q只能在 軸兩側(cè)。
軸兩側(cè)。
不妨設(shè) ,則
,則 ,顯然
,顯然
∵ 是以O(shè)為直角頂點(diǎn)的直角三角形,∴
是以O(shè)為直角頂點(diǎn)的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設(shè)要求的兩點(diǎn)P、Q;
(*)若方程(*)有解,存在滿足題設(shè)要求的兩點(diǎn)P、Q;
若方程(*)無(wú)解,不存在滿足題設(shè)要求的兩點(diǎn)P、Q.
若 ,則
,則 代入(*)式得:
代入(*)式得:
即 ,而此方程無(wú)解,因此
,而此方程無(wú)解,因此 。此時(shí)
。此時(shí) ,
,
代入(*)式得:  即
即 (**)
(**)
令
 ,則
,則
∴ 在
在 上單調(diào)遞增, ∵
上單調(diào)遞增, ∵  ∴
∴ ,∴
,∴ 的取值范圍是
的取值范圍是 。
。
∴對(duì)于 ,方程(**)總有解,即方程(*)總有解。
,方程(**)總有解,即方程(*)總有解。
因此,對(duì)任意給定的正實(shí)數(shù) ,曲線
,曲線 上存在兩點(diǎn)P、Q,使得
上存在兩點(diǎn)P、Q,使得 是以O(shè)為直角頂點(diǎn)的直角三角形,且此三角形斜邊中點(diǎn)在
是以O(shè)為直角頂點(diǎn)的直角三角形,且此三角形斜邊中點(diǎn)在 軸上
軸上
已知函數(shù)
(1)若函數(shù) 的圖象經(jīng)過(guò)P(3,4)點(diǎn),求a的值;
的圖象經(jīng)過(guò)P(3,4)點(diǎn),求a的值;
(2)比較 大小,并寫出比較過(guò)程;
大小,并寫出比較過(guò)程;
(3)若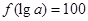 ,求a的值.
,求a的值.
【解析】本試題主要考查了指數(shù)函數(shù)的性質(zhì)的運(yùn)用。第一問(wèn)中,因?yàn)楹瘮?shù) 的圖象經(jīng)過(guò)P(3,4)點(diǎn),所以
的圖象經(jīng)過(guò)P(3,4)點(diǎn),所以 ,解得
,解得 ,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012061921574878204718/SYS201206192159225008161918_ST.files/image007.png">,所以
,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012061921574878204718/SYS201206192159225008161918_ST.files/image007.png">,所以 .
.
(2)問(wèn)中,對(duì)底數(shù)a進(jìn)行分類討論,利用單調(diào)性求解得到。
(3)中,由 知,
知, .,指對(duì)數(shù)互化得到
.,指對(duì)數(shù)互化得到 ,,所以
,,所以 ,解得所以,
,解得所以, 或
或  .
.
解:⑴∵函數(shù) 的圖象經(jīng)過(guò)
的圖象經(jīng)過(guò) ∴
∴ ,即
,即 . … 2分
. … 2分
又 ,所以
,所以 .
………… 4分
.
………… 4分
⑵當(dāng) 時(shí),
時(shí), ;
;
當(dāng) 時(shí),
時(shí), . ……………… 6分
. ……………… 6分
因?yàn)椋?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012061921574878204718/SYS201206192159225008161918_ST.files/image021.png">,
當(dāng) 時(shí),
時(shí), 在
在 上為增函數(shù),∵
上為增函數(shù),∵ ,∴
,∴ .
.
即 .當(dāng)
.當(dāng) 時(shí),
時(shí), 在
在 上為減函數(shù),
上為減函數(shù),
∵ ,∴
,∴ .即
.即 . …………………… 8分
. …………………… 8分
⑶由 知,
知, .所以,
.所以, (或
(或 ).
).
∴ .∴
.∴ , … 10分
, … 10分
∴ 或
或
 ,所以,
,所以, 或
或  .
.
函數(shù) 在同一個(gè)周期內(nèi),當(dāng)
在同一個(gè)周期內(nèi),當(dāng) 時(shí),
時(shí), 取最大值1,當(dāng)
取最大值1,當(dāng) 時(shí),
時(shí), 取最小值
取最小值 。
。
(1)求函數(shù)的解析式
(2)函數(shù) 的圖象經(jīng)過(guò)怎樣的變換可得到
的圖象經(jīng)過(guò)怎樣的變換可得到 的圖象?
的圖象?
(3)若函數(shù) 滿足方程
滿足方程 求在
求在 內(nèi)的所有實(shí)數(shù)根之和.
內(nèi)的所有實(shí)數(shù)根之和.
【解析】第一問(wèn)中利用
又因
又
 函數(shù)
函數(shù)
第二問(wèn)中,利用 的圖象向右平移
的圖象向右平移 個(gè)單位得
個(gè)單位得 的圖象
的圖象
再由 圖象上所有點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的
圖象上所有點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的 .縱坐標(biāo)不變,得到
.縱坐標(biāo)不變,得到 的圖象,
的圖象,
第三問(wèn)中,利用三角函數(shù)的對(duì)稱性, 的周期為
的周期為
 在
在 內(nèi)恰有3個(gè)周期,
內(nèi)恰有3個(gè)周期,
并且方程 在
在 內(nèi)有6個(gè)實(shí)根且
內(nèi)有6個(gè)實(shí)根且
同理, 可得結(jié)論。
可得結(jié)論。
解:(1)
又因
又
 函數(shù)
函數(shù)
(2) 的圖象向右平移
的圖象向右平移 個(gè)單位得
個(gè)單位得 的圖象
的圖象
再由 圖象上所有點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的
圖象上所有點(diǎn)的橫坐標(biāo)變?yōu)樵瓉?lái)的 .縱坐標(biāo)不變,得到
.縱坐標(biāo)不變,得到 的圖象,
的圖象,
(3) 的周期為
的周期為
 在
在 內(nèi)恰有3個(gè)周期,
內(nèi)恰有3個(gè)周期,
并且方程 在
在 內(nèi)有6個(gè)實(shí)根且
內(nèi)有6個(gè)實(shí)根且
同理,
故所有實(shí)數(shù)之和為
下列敘述中,是離散型隨機(jī)變量的為( )
A.某人早晨在車站等出租車的時(shí)間
B.將一顆均勻硬幣擲十次,出現(xiàn)正面或反面的次數(shù)
C.連續(xù)不斷的射擊,首次命中目標(biāo)所需要的次數(shù)
D.袋中有2個(gè)黑球6個(gè)紅球,任取2個(gè),取得一個(gè)紅球的可能性 3.C.解析:由條件f(a)>0,f(b)>0僅知道二次函數(shù)圖象過(guò)x軸上方兩點(diǎn),據(jù)此畫圖會(huì)出現(xiàn)多種情況與x軸交點(diǎn)橫坐標(biāo)在(a,b)上可能有0個(gè)、1個(gè)或2個(gè),因此選C
問(wèn)題:將y=2x的圖象向________平行移動(dòng)________個(gè)單位,再作關(guān)于直線y=x對(duì)稱的圖象,可得函數(shù)y=log2(x+1)的圖象.
對(duì)于此問(wèn)題,甲、乙、丙三位同學(xué)分別給出了不同的解法:
甲:在同一坐標(biāo)系內(nèi)分別作y=2x與y=log2(x+1)的圖象,直接觀察,可知向下平行移動(dòng)1個(gè)單位即得.
乙:與函數(shù)y=log2(x+1)的圖象關(guān)于直線y=x對(duì)稱的曲線是它的反函數(shù)y=2x-1的圖象,為了得到它,只需將y=2x的圖象向下平移1個(gè)單位.
丙:由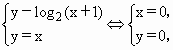 所以點(diǎn)(0,0)在函數(shù)y=log2(x+1)的圖象上,(0,0)點(diǎn)關(guān)于y=x的對(duì)稱的點(diǎn)還是其本身.函數(shù)y=2x的圖象向左或向右或向上平行移動(dòng)都不會(huì)過(guò)(0,0)點(diǎn),因此只能向下平行移動(dòng)1個(gè)單位.
所以點(diǎn)(0,0)在函數(shù)y=log2(x+1)的圖象上,(0,0)點(diǎn)關(guān)于y=x的對(duì)稱的點(diǎn)還是其本身.函數(shù)y=2x的圖象向左或向右或向上平行移動(dòng)都不會(huì)過(guò)(0,0)點(diǎn),因此只能向下平行移動(dòng)1個(gè)單位.
你贊同誰(shuí)的解法?你還有其他更好的解法嗎?
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com