
題目列表(包括答案和解析)
已知數列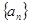 的前
的前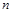 項和
項和 是二項式
是二項式 展開式中含
展開式中含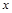 奇次冪的系數和.
奇次冪的系數和.
(1)求數列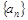 的通項公式;
的通項公式;
(2)設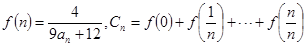 ,求
,求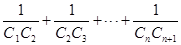 的值.
的值.
| x |
| 1 | |||
|
(07年遼寧卷文)![]() 展開式中含
展開式中含![]() 的整數次冪的項的系數之和為 (用數字作答).
的整數次冪的項的系數之和為 (用數字作答).
(07年遼寧卷文)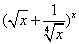 展開式中含
展開式中含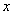 的整數次冪的項的系數之和為 (用數字作答).
的整數次冪的項的系數之和為 (用數字作答).
 一、選擇題
一、選擇題
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
A
C
B
D
C
B
A
B
D
A
二、填空題
 13.
13. 14. 7500 15. (-1,1)
14. 7500 15. (-1,1)
 16.
16.  17.45o 18.
17.45o 18.
 三、解答題
三、解答題
 19解:(Ⅰ)
19解:(Ⅰ)

┅┅┅┅┅┅┅4分
因為 ,所以
,所以 ,所以
,所以 ,
,
即 的取值范圍為
的取值范圍為 ┅┅┅┅┅┅┅6分
┅┅┅┅┅┅┅6分
(Ⅱ)因為 ,所以
,所以 ┅┅┅┅┅┅┅8分
┅┅┅┅┅┅┅8分

 所以
所以 的最小值為
的最小值為 ,當
,當 即
即 為等邊三角形時取到. ┅┅┅┅┅┅┅12分
為等邊三角形時取到. ┅┅┅┅┅┅┅12分
 20(Ⅰ)證明(方法一)取
20(Ⅰ)證明(方法一)取 中點
中點 ,連接
,連接 ,因為
,因為 分別為
分別為 中點,所以
中點,所以 ,┅┅┅┅┅┅┅3分
,┅┅┅┅┅┅┅3分
所以 ,所以四邊形
,所以四邊形 為平行四邊形,所以
為平行四邊形,所以 ,又因為
,又因為 ,所以
,所以 面
面 ;┅┅┅┅┅┅┅6分
;┅┅┅┅┅┅┅6分
(方法二)取 中點
中點 ,連接
,連接 ,
,
 因為
因為 分別為
分別為 中點,所以
中點,所以
又因為 分別為
分別為 中點,所以
中點,所以 ┅┅┅┅┅┅┅3分
┅┅┅┅┅┅┅3分
且 ,
,

 所以面
所以面 面
面 ,
,
又 面
面 ,所以
,所以 面
面 ┅┅┅┅┅┅6分
┅┅┅┅┅┅6分
(方法三)取 中點
中點 ,連接
,連接 ,
,
由題可得 ,又因為面
,又因為面 面
面 ,
,
所以 面
面 ,又因為菱形
,又因為菱形 中
中 ,所以
,所以 .
.
可以建立如圖所示的空間直角坐標系
┅┅┅┅┅┅┅7分
不妨設 ,
,
可得 ,
,
 ,
, ,
, ,
, ,所以
,所以
所以 ,┅┅┅┅┅┅┅9分
,┅┅┅┅┅┅┅9分
 設面
設面 的一個法向量為
的一個法向量為 ,則
,則 ,不妨取
,不妨取 ,則
,則 ,所以
,所以 ,又因為
,又因為 面
面 ,所以
,所以 面
面 .
.
┅┅┅┅┅┅┅12分
 (Ⅱ)(方法一)
(Ⅱ)(方法一)
過 點作
點作 的垂線
的垂線 交
交 于
于 ,連接
,連接 .
.
因為 ,
,
所以 ,所以
,所以 面
面 ,
,
所以 為二面角
為二面角 的平面角. ┅┅┅┅┅┅┅8分
的平面角. ┅┅┅┅┅┅┅8分
因為面 面
面 ,所以
,所以 點在面
點在面 上的射影落在
上的射影落在 上,所以
上,所以 ,
,
所以 ,不妨設
,不妨設 ,所以
,所以 ,同理可得
,同理可得 .┅┅┅┅┅┅┅10分
.┅┅┅┅┅┅┅10分
所以 ,所以二面角
,所以二面角 的大小為
的大小為 ┅┅┅┅┅┅┅12分
┅┅┅┅┅┅┅12分
(方法二)由(Ⅰ)方法三可得 ,設面
,設面 的一個法向量為
的一個法向量為 ,則
,則 ,不妨取
,不妨取 ,則
,則 .
.
┅┅┅┅┅┅┅8分
 又
又 ,設面
,設面 的一個法向量為
的一個法向量為 ,則
,則 ,不妨取
,不妨取 ,則
,則 .┅┅┅┅┅┅┅10分
.┅┅┅┅┅┅┅10分
所以 ,因為二面角
,因為二面角 為銳角,所以二面角
為銳角,所以二面角 的大小為
的大小為 ┅┅┅┅┅┅┅12分
┅┅┅┅┅┅┅12分
21解:
(Ⅰ)從盒中一次性取出三個球,取到白球個數的分布列是超幾何分布,┅┅┅┅┅┅┅1分
所以期望為 ,所以
,所以 ,即盒中有 3個紅球,2 個白球.┅┅┅┅┅┅┅3分
,即盒中有 3個紅球,2 個白球.┅┅┅┅┅┅┅3分
(Ⅱ)由題可得 的取值為0,1,2,3.
的取值為0,1,2,3.

 ,
,
 =
= ,
,
 ,
,


所以 的分布列為
的分布列為

0
1
2
3
P




┅┅┅┅┅┅┅11分
E =
=
答:紅球的個數為2, 的數學期望為2 ┅┅┅┅┅┅┅12分
的數學期望為2 ┅┅┅┅┅┅┅12分
22解:(Ⅰ)由 可得
可得 ,┅┅┅┅┅┅┅2分
,┅┅┅┅┅┅┅2分
即 ,所以
,所以 ,┅┅┅┅┅┅┅4分
,┅┅┅┅┅┅┅4分
又 ,所以
,所以 ,
,
所以 是等差數列,首項為
是等差數列,首項為 ,公差為1┅┅┅┅┅┅┅6分
,公差為1┅┅┅┅┅┅┅6分
(Ⅱ)由(Ⅰ)可得 ,即
,即 ┅┅┅┅┅┅┅7分
┅┅┅┅┅┅┅7分
令 ①
①
則 ②┅┅┅┅┅┅9分
②┅┅┅┅┅┅9分
①-②可得
所以 ,所以
,所以 ┅┅12分
┅┅12分
23解:(Ⅰ)由題意可知,可行域是以 及點
及點 為頂點的三角形,
為頂點的三角形,
∵ ,∴
,∴ 為直角三角形, ┅┅┅┅┅┅┅2分
為直角三角形, ┅┅┅┅┅┅┅2分
 ∴外接圓C以原點O為圓心,線段A1A2為直徑,故其方程為
∴外接圓C以原點O為圓心,線段A1A2為直徑,故其方程為 .
.
∵2b=4,∴b=2.又 ,可得
,可得 .
.
∴所求橢圓C1的方程是 .
┅┅┅┅┅┅┅4分
.
┅┅┅┅┅┅┅4分
(Ⅱ)設A(x1,y1),B(x2,y2), ,OA的斜率為
,OA的斜率為 ,則PA的斜率為
,則PA的斜率為 ,則PA的方程為:
,則PA的方程為: 化簡為:
化簡為: ,
,
同理PB的方程為 ┅┅┅┅┅┅┅6分
┅┅┅┅┅┅┅6分
又PA、PB同時過P點,則x1x0+y1y0=4,x2x0+y2y0=4,
∴AB的直線方程為:x0x+y0y=4 ┅┅┅┅┅┅┅8分
(或者求出以OP為直徑的圓,然后求出該圓與圓C的公共弦所在直線方程即為AB的方程)
從而得到 、
、
所以  ┅┅┅┅┅┅┅8分
┅┅┅┅┅┅┅8分


當且僅當 .
┅┅┅┅┅┅┅12分
.
┅┅┅┅┅┅┅12分
(或者利用橢圓的參數方程 、函數求最值等方法求
、函數求最值等方法求 的最大值)
的最大值)
24解:(Ⅰ) ┅┅┅┅┅┅┅2分
┅┅┅┅┅┅┅2分
①當 ,即
,即 ,在
,在 上有
上有 ,所以
,所以 在
在 單調遞增;┅┅┅┅┅┅┅4分
單調遞增;┅┅┅┅┅┅┅4分
 ②當
②當 ,即
,即 ,當
,當 時,在
時,在 上有
上有 ,所以
,所以 在
在 單調遞增;當
單調遞增;當 時,在
時,在 上有
上有 ,所以
,所以 在
在 單調遞增;┅┅┅┅┅┅┅6分
單調遞增;┅┅┅┅┅┅┅6分
③當 ,即
,即
當 時,函數
時,函數 對稱軸在y軸左側,且
對稱軸在y軸左側,且 ,所以在
,所以在 上有
上有 ,所以
,所以 在
在 單調遞增;┅┅┅┅┅┅┅8分
單調遞增;┅┅┅┅┅┅┅8分
當 時,函數
時,函數 對稱軸在
對稱軸在 右側,且
右側,且 ,
,
 兩個根分別為
兩個根分別為 ,所以在
,所以在 上有
上有 ,即
,即 在
在 單調遞增;在
單調遞增;在 上有
上有 ,即
,即 在
在 單調遞減.
單調遞減.
綜上: 時,
時, 在
在 單調遞增;
單調遞增; 時,
時, 在
在 單調遞增,在
單調遞增,在 單調遞減. ┅┅┅┅┅┅┅10分
單調遞減. ┅┅┅┅┅┅┅10分
(Ⅱ)由(Ⅰ)可知當 時,
時, 有極大值
有極大值 ,極小值
,極小值 ,所以
,所以
 ,又因為
,又因為 ,
,
┅┅┅12分
所以

=
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com