
題目列表(包括答案和解析)
已知函數 的最小值為0,其中
的最小值為0,其中
(Ⅰ)求 的值;
的值;
(Ⅱ)若對任意的 有
有 ≤
≤ 成立,求實數
成立,求實數 的最小值;
的最小值;
(Ⅲ)證明 (
( ).
).
【解析】(1)解:
 的定義域為
的定義域為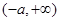

由 ,得
,得
當x變化時, ,
, 的變化情況如下表:
的變化情況如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
極小值 |
|
因此, 在
在 處取得最小值,故由題意
處取得最小值,故由題意 ,所以
,所以
(2)解:當 時,取
時,取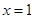 ,有
,有 ,故
,故 時不合題意.當
時不合題意.當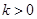 時,令
時,令 ,即
,即

令 ,得
,得
①當 時,
時, ,
, 在
在 上恒成立。因此
上恒成立。因此 在
在 上單調遞減.從而對于任意的
上單調遞減.從而對于任意的 ,總有
,總有 ,即
,即 在
在 上恒成立,故
上恒成立,故 符合題意.
符合題意.
②當 時,
時, ,對于
,對于 ,
, ,故
,故 在
在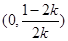 上單調遞增.因此當取
上單調遞增.因此當取 時,
時, ,即
,即 不成立.
不成立.
故 不合題意.
不合題意.
綜上,k的最小值為 .
.
(3)證明:當n=1時,不等式左邊= =右邊,所以不等式成立.
=右邊,所以不等式成立.
當 時,
時,


在(2)中取 ,得
,得
 ,
,
從而

所以有





綜上,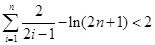 ,
,
(1)y=lg(x-2)+1;
(2)y=![]() .
.
設數列 的各項均為正數.若對任意的
的各項均為正數.若對任意的 ,存在
,存在 ,使得
,使得 成立,則稱數列
成立,則稱數列 為“Jk型”數列.
為“Jk型”數列.
(1)若數列 是“J2型”數列,且
是“J2型”數列,且 ,
, ,求
,求 ;
;
(2)若數列 既是“J3型”數列,又是“J4型”數列,證明:數列
既是“J3型”數列,又是“J4型”數列,證明:數列 是等比數列.
是等比數列.
【解析】1)中由題意,得 ,
, ,
, ,
, ,…成等比數列,且公比
,…成等比數列,且公比 ,
,
所以.
(2)中證明:由{ }是“j4型”數列,得
}是“j4型”數列,得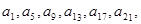 ,…成等比數列,設公比為t. 由{
,…成等比數列,設公比為t. 由{ }是“j3型”數列,得
}是“j3型”數列,得
 ,…成等比數列,設公比為
,…成等比數列,設公比為 ;
;
 ,…成等比數列,設公比為
,…成等比數列,設公比為 ;
;
 …成等比數列,設公比為
…成等比數列,設公比為 ;
;
(1)已知f(x)=x2+2x,求f(2x+1);
(2)已知f(![]() -1)=x+2
-1)=x+2![]() ,求f(x);
,求f(x);
(3)已知f(x)-![]() )=3x+2,求f(x).
)=3x+2,求f(x).
某種型號的汽車在勻速行駛中每小時耗油量 關于行駛速度
關于行駛速度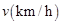 的函數解析式可以表示為:
的函數解析式可以表示為: .已知甲、乙兩地相距
.已知甲、乙兩地相距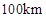 ,設汽車的行駛速度為
,設汽車的行駛速度為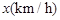 ,從甲地到乙地所需時間為
,從甲地到乙地所需時間為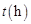 ,耗油量為
,耗油量為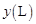 .
.
(1)求函數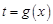 及
及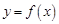 ;
;
(2)求當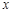 為多少時,
為多少時,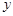 取得最小值,并求出這個最小值.
取得最小值,并求出這個最小值.
【解析】(1) 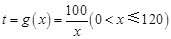 ,根據
,根據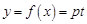 可求出y=f(x).
可求出y=f(x).
(2)求導,根據導數確定其最小值.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com