
題目列表(包括答案和解析)
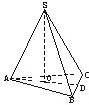 如圖,設三棱錐S-ABC的三個側棱與底面ABC所成的角都是60°,又∠BAC=60°,且SA⊥BC.
如圖,設三棱錐S-ABC的三個側棱與底面ABC所成的角都是60°,又∠BAC=60°,且SA⊥BC.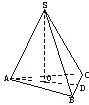 如圖,設三棱錐S-ABC的三個側棱與底面ABC所成的角都是60°,又∠BAC=60°,且SA⊥BC.
如圖,設三棱錐S-ABC的三個側棱與底面ABC所成的角都是60°,又∠BAC=60°,且SA⊥BC.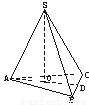

 (2010•上饒二模)如圖,設三棱錐O-ABC的三條側棱OA,OB,OC兩兩垂直,三個側面與底面所成的二面角O-AB-C,O-BC-A,O-CA-B分別等于α1,α2,α3.記△OAB,△OBC,△OCA,△ABC的面積分別為S1,S2,S3,S,則下列四個命題:(1)Si=Scosαi(i=1,2,3)(2)若∠BAO=∠CAO=45°,則∠BAC=60°(3)S2=S12+S22+S32.(4)α1,α2,α3的取值可以分別是30°,45°,60°.
(2010•上饒二模)如圖,設三棱錐O-ABC的三條側棱OA,OB,OC兩兩垂直,三個側面與底面所成的二面角O-AB-C,O-BC-A,O-CA-B分別等于α1,α2,α3.記△OAB,△OBC,△OCA,△ABC的面積分別為S1,S2,S3,S,則下列四個命題:(1)Si=Scosαi(i=1,2,3)(2)若∠BAO=∠CAO=45°,則∠BAC=60°(3)S2=S12+S22+S32.(4)α1,α2,α3的取值可以分別是30°,45°,60°.湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com