
題目列表(包括答案和解析)
| ||
| 2 |
| 2 |
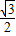
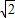 +2cosx≥0
+2cosx≥0已知等差數列{an}的首項為4,公差為4,其前n項和為Sn,則數列 {![]() }的前n項和為( )
}的前n項和為( )
|
| A. |
| B. |
| C. |
| D. |
|
| 考點: | 數列的求和;等差數列的性質. |
| 專題: | 等差數列與等比數列. |
| 分析: | 利用等差數列的前n項和即可得出Sn,再利用“裂項求和”即可得出數列 { |
| 解答: | 解:∵Sn=4n+ ∴ ∴數列 { 故選A. |
| 點評: | 熟練掌握等差數列的前n項和公式、“裂項求和”是解題的關鍵. |
如圖所示為某三角函數圖象的一段.
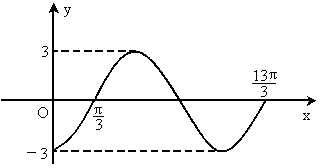
(1)用正弦函數寫出其解析式;
(2)求與這個函數關于直線x=2n對稱的函數解析式.
如圖為某三角函數圖象的一段:
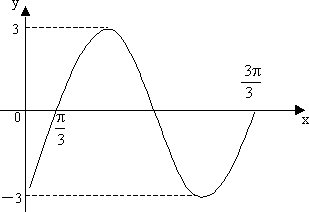
(1)用正弦函數寫出其解析式;
(2)求與這個函數關于直線x=2π對稱的函數解析式.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com