
題目列表(包括答案和解析)
| f(x2)-f(x1) |
| x2-x1 |
| f(b)-f(a) |
| b-a |
| b-a |
| b |
| b |
| a |
| b-a |
| a |
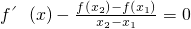 在(x1,x2)恒有實數解
在(x1,x2)恒有實數解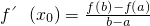 .如我們所學過的指、對數函數,正、余弦函數等都符合拉格朗日中值定理條件.試用拉格朗日中值定理證明:
.如我們所學過的指、對數函數,正、余弦函數等都符合拉格朗日中值定理條件.試用拉格朗日中值定理證明: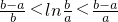 (可不用證明函數的連續性和可導性).
(可不用證明函數的連續性和可導性).已知函數f(x)=mx3+nx2(m、n∈R ,m≠0)的圖像在(2,f(2))處的切線與x軸平行.
(1)求n,m的關系式并求f(x)的單調減區間;
(2)證明:對任意實數0<x1<x2<1, 關于x的方程:
![]() 在(x1,x2)恒有實數解
在(x1,x2)恒有實數解
(3)結合(2)的結論,其實我們有拉格朗日中值定理:若函數f(x)是在閉區間[a,b]上連續不斷的函數,且在區間(a,b)內導數都存在,則在(a,b)內至少存在一點x0,使得![]() .如我們所學過的指、對數函數,正、余弦函數等都符合拉格朗日中值定理條件.試用拉格朗日中值定理證明:
.如我們所學過的指、對數函數,正、余弦函數等都符合拉格朗日中值定理條件.試用拉格朗日中值定理證明:
當0<a<b時,![]() (可不用證明函數的連續性和可導性)
(可不用證明函數的連續性和可導性)
 在(x1,x2)恒有實數解
在(x1,x2)恒有實數解 .如我們所學過的指、對數函數,正、余弦函數等都符合拉格朗日中值定理條件.試用拉格朗日中值定理證明:
.如我們所學過的指、對數函數,正、余弦函數等都符合拉格朗日中值定理條件.試用拉格朗日中值定理證明: (可不用證明函數的連續性和可導性).
(可不用證明函數的連續性和可導性).角
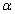 的頂點在原點,始邊與x軸的正半軸重合,終邊在函數y=-2x(x≤0)的圖像上.
的頂點在原點,始邊與x軸的正半軸重合,終邊在函數y=-2x(x≤0)的圖像上.
(1)
求cos 和sin(
和sin( +
+ )的值.
)的值.
(2)
能否求出角2k +
+ (k∈Z),-
(k∈Z),- ,2
,2 -
- ,
, ±
± ,
, ±
± 的正弦函數值、余弦函數值?若能,求出值,若不能,請說明理由.
的正弦函數值、余弦函數值?若能,求出值,若不能,請說明理由.湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com