日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

（本小題滿分12分）

甲乙兩位玩家在進行“石頭、剪子、布”的游戲，假設兩人在游戲時出示三種手勢是等可能的。

（Ⅰ）求在1次游戲中甲勝乙的概率；

（Ⅱ）若甲乙雙方共進行了3次游戲，隨機變量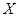表示甲勝乙的次數，求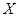的分布列和數學期望．

 

（本小題滿分12分）

甲乙兩個班級進行一門課程的考試，按照學生考試成績優秀和不優秀統計成績后，得到如下的列聯表：

班級與成績列聯表

	優 秀	不優秀
甲 班	10	35
乙 班	7	38

根據列聯表的獨立性檢驗，能否在犯錯誤的概率不超過0.01的前提下認為成績與班級有關系？

 附：  

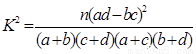
	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

 

 

 

 

 

 

 

（本小題滿分12分）甲乙兩個學校高三年級分別有1200人，1000人，為了了解兩個學校全體高三年級學生在該地區六校聯考的數學成績情況，采用分層抽樣方法從兩個學校一共抽取了110名學生的數學成績，并作出了頻數分布統計表如下：

 

分組	[70,80）	[80,90）	[90,100）	[100,110）
頻數	3	4	8	15
分組	[110,120）	[120,130）	[130,140）	[140,150]
頻數	15	x	3	2

    甲校：

 

 

分組	[70,80）	[80,90）	[90,100）	[100,110）
頻數	1	2	8	9
分組	[110,120）	[120,130）	[130,140）	[140,150]
頻數	10	10	y	3

    乙校：

 

 

 

（Ⅰ）計算x，y的值。

（Ⅱ）若規定考試成績在[120,150]內為優秀，請分別估計兩個學校數學成績的優秀率。

 

	甲校	乙校	總計
優秀
非優秀
總計

 

 

 

 

 

 

（Ⅲ）由以上統計數據填寫右面2×2列聯表，并判斷是否有90%的把握認為兩個學校的數學成績有差異。

參考數據與公式：

由列聯表中數據計算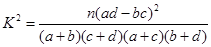

臨界值表

 

 

 

(本小題滿分12分）

甲乙兩個學校高三年級分別有1100人，1000人，為了了解兩個學校全體高三年級學生在該地區二模考試的數學成績情況，采用分層抽樣方法從兩個學校一共抽取了 105名學生的數學成績，并作出了如下的頻數分布統計表，規定考試成績在[120，150]內為優秀，甲校：

乙校：

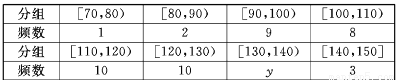
(I )計算x，y的值;

(II)由以上統計數據填寫右面2X2列聯表，若按是否優秀來判斷，是否有97.5% 的把握認為兩個學校的數學成績有差異.

(III)根據抽樣結果分別估計甲校和乙校的優秀率；若把頻率作為概率，現從乙校學生中任取3人，求優秀學生人數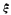的分布列和數學期望;

附：

 

（本小題滿分12分）

        甲乙兩個學校高三年級分別為1100人，1000人，為了統計兩個學校在地區二模考試的數學科目成績，采用分層抽樣抽取了105名學生的成績，并作出了部分頻率分布表如下：（規定考試成績在[120，150]內為優秀）

甲校：

分組								[140,150]
頻數	2	3	10	15	15	x	3	1

乙校：

分組					[來源:學§科§網Z§X§X§K]			[140,150]
頻數	1	2	9	8	10	10	y	3

   （1）計算x，y的值，并分別估計兩上學校數學成績的優秀率；

   （2）由以上統計數據填寫下面2×2列聯表，并判斷是否有97.5%的把握認為兩個學校的數學成績有差異.

	甲校	乙校	總計
優秀
非優秀
總計

附：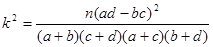

	0．10	0．025	0．010
	2．706	5．024	6．635