
題目列表(包括答案和解析)
 如圖,在長方體ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M為B1C1上一點,且B1M=2,點N在線段A1D上,A1D⊥AN,求: (1)
如圖,在長方體ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M為B1C1上一點,且B1M=2,點N在線段A1D上,A1D⊥AN,求: (1) ![]() ;
;
(2) 直線AD與平面ANM所成的角的大小;
(3) 平面ANM與平面ABCD所成角(銳角)的大小.
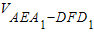 ,V2=
,V2= ,V3=
,V3=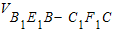 .若V1:V2:V3=1:3:1,則截面A1EFD1的面積為( )
.若V1:V2:V3=1:3:1,則截面A1EFD1的面積為( )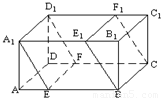
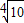

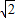
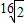
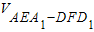 ,V2=
,V2= ,V3=
,V3=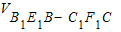 .若V1:V2:V3=1:3:1,則截面A1EFD1的面積為( )
.若V1:V2:V3=1:3:1,則截面A1EFD1的面積為( )
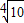
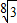

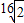
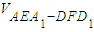 ,V2=
,V2=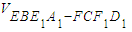 ,V3=
,V3=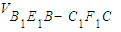 .若V1:V2:V3=1:3:1,則截面A1EFD1的面積為( )
.若V1:V2:V3=1:3:1,則截面A1EFD1的面積為( )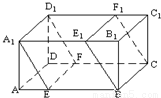
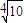

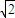
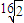
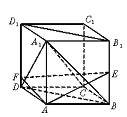
(1)求證:A1C⊥平面AEF;
(2)若規定兩個平面所成的角是這兩個平面所組成的二面角中的銳角(或直角).則在空間中有定理:若兩條直線分別垂直于兩個平面,則這兩條直線所成的角與這兩個平面所成的角相等.
試根據上述定理,在AB=4,AD=3,AA1=5時,求平面AEF與平面D1B1BD所成角的大小.(用反三角函數值表示)
一、選擇題
題 號
1
2
3
4
5
6
7
8
9
10
11
12
答 案
D
C
A
D
D
B
A
B
C
D
A
C
二、填空題
13. {x|x≤?2或x=1} 14. 7 15. 18
16. .files/image106.gif)
三、解答題(共74分)
17.(1)∵這名學生在第一、二個路口沒遇到紅燈,第三個路口遇到紅燈。
∴概率P=(1?.files/image064.gif) )(1?
)(1?.files/image064.gif) )×
)×.files/image064.gif) =
=.files/image109.gif)
(2)(理).files/image111.gif) ∴
∴.files/image113.gif)
.files/image115.gif)
(文).files/image117.gif)
18.∵α∈(0,.files/image085.gif) ),β∈(
),β∈(.files/image085.gif) ,2
,2.files/image085.gif) ), ∴
), ∴.files/image119.gif) ,
,.files/image121.gif)
又.files/image123.gif) ,
,
.files/image125.gif) ∴
∴.files/image127.gif)
又.files/image129.gif)
.files/image131.gif) 且
且.files/image133.gif) ,
,.files/image135.gif)
∴.files/image137.gif) ∴
∴.files/image139.gif)
∴.files/image141.gif)
19.解(1)令.files/image143.gif) 則2bx2+x+a=0
則2bx2+x+a=0
由題意知:x=1,2是上方程兩根,由韋達定理:
.files/image145.gif) ∴
∴.files/image147.gif)
(2)由(1)知:.files/image149.gif)
令.files/image151.gif) 解得:x<0或1<x<2
解得:x<0或1<x<2
∴f(x)的單調增區間為(1,2) 減區間是(0,1)和(2,+.files/image153.gif) )
)
(3)由(2)知:f(x)在x1=1處取極小值,在x2=2處取極大值。
20.(1)以A為原點,AB、AD、AA1所在直線為x軸,y軸,z軸。
則D(0,8,0),A1(0,0,4),M(5,2,4)
.files/image154.gif) ∴
∴.files/image156.gif)
.files/image158.gif)
∵.files/image160.gif) ∴
∴.files/image162.gif)
(2)由(1)知A1D⊥AM,又由已知A1D⊥AN,
∴A1D⊥平面AMN,垂足為N。
因此AD與平面所成的角即是∠DAN。
易知∠DAN = AA1D = arctan2
(3)∵AA1⊥平面ABCD,A1N⊥平面AMN,
∴.files/image164.gif) 和
和.files/image166.gif) 分別成為平面ABCD和平面AMN的法向量。
分別成為平面ABCD和平面AMN的法向量。
設平面AMN與平面ABCD所成的角(銳角)為.files/image168.gif) ,則
,則
.files/image168.gif) =(
=(.files/image164.gif) ,
,.files/image166.gif) )=∠AA1N
= AA1D = arccos
)=∠AA1N
= AA1D = arccos.files/image170.gif)
21.(1)解:設P(a,0),Q(0,b)
則:.files/image172.gif) ∴
∴.files/image174.gif)
設M(x,y)∵.files/image176.gif)
∴.files/image178.gif)
.files/image180.gif)
∴.files/image182.gif)
(2)解法一:設A(a,b),.files/image184.gif) ,
,.files/image186.gif) (x1≠x2)
(x1≠x2)
則:直線SR的方程為:.files/image188.gif) ,即4y = (x1+x2)x-x1x2
,即4y = (x1+x2)x-x1x2
∵A點在SR上,∴4b=(x1+x2)a-x1x2 ①
對.files/image182.gif) 求導得:y′=
求導得:y′=.files/image057.gif) x
x
∴拋物線上S、R處的切線方程為:
.files/image192.gif) 即4
即4.files/image194.gif) ②
②
.files/image196.gif) 即4
即4.files/image198.gif) ③
③
聯立②③,并解之得.files/image200.gif) ,代入①得:ax-2y-2b=0
,代入①得:ax-2y-2b=0
故:B點在直線ax-2y-2b=0上
解法二:設A(a,b)
當過點A的直線斜率不存在時l與拋物線有且僅有一個公共點,與題意不符,可設直線SR的方程為y-b=k(x-a)
與.files/image182.gif) 聯立消去y得:x2-4kx+4ak-4b=0
聯立消去y得:x2-4kx+4ak-4b=0
設.files/image184.gif) ,
,.files/image186.gif) (x1≠x2)
(x1≠x2)
則由韋達定理:.files/image204.gif)
又過S、R點的切線方程分別為:.files/image206.gif) ,
,.files/image208.gif)
聯立,并解之得.files/image210.gif) (k為參數)
(k為參數)
消去k,得:ax-2y-2b=0
故:B點在直線2ax-y-b=0上
22.解(1)令m=-1,n=0則:f(?1)=f(?1)f(0),而f(?1)>1 ∴f(0)=1
令m=x>0,n= ?x<0則f(x?x)=f(x)?f(?x)=1
∴f(x)=.files/image212.gif)
.files/image214.gif) (0,1),即x>0時0<f(x)<1
(0,1),即x>0時0<f(x)<1
設x1<x2則x2?x1=0 ∴0<f (x2?x1)?f (x1)?f (x1)=f (x1)[f (x2?x1)?1]<0 ∴f(x)<f(x1)
即y = f (x)在R上單調遞減
(2)由f(an+1)=.files/image216.gif) ,n
,n.files/image214.gif) N* 得:f(an+1)?f(?2?an)
=1
N* 得:f(an+1)?f(?2?an)
=1
∴f(an+1?an?2) = f (0) 由(1)知:an+1?an?2=0
即an+1?an=2(n.files/image214.gif) N*) ∴{an}是首項為a1=1,公差為2的等差數列
N*) ∴{an}是首項為a1=1,公差為2的等差數列
∴an=2n?1
(3)假設存在正數k,使(1+.files/image218.gif)
.files/image220.gif) 對n
對n.files/image214.gif) N*恒成立
N*恒成立
記F(n)=.files/image222.gif)
即.files/image224.gif) ∴F(n)是遞增數列,F(1)為最小值。
∴F(n)是遞增數列,F(1)為最小值。
由F(n).files/image226.gif) 恒成立知k
恒成立知k.files/image228.gif) ∴kmax =
∴kmax = .files/image230.gif) .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com