
題目列表(包括答案和解析)
甲、乙等五名志愿者被隨機地分到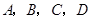 四個不同的崗位服務,每個崗位至少有一名志愿者.
四個不同的崗位服務,每個崗位至少有一名志愿者.
(Ⅰ)求甲、乙兩人同時參加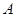 崗位服務的概率;
崗位服務的概率;
(Ⅱ)設隨機變量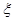 為這五名志愿者中參加
為這五名志愿者中參加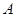 崗位服務的人數,求
崗位服務的人數,求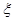 的分布列.
的分布列.
甲、乙等五名奧運志愿者被隨機地分到![]() 四個不同的崗位服務,每個崗位至少有一名志愿者.⑴求甲、乙兩人同時參加
四個不同的崗位服務,每個崗位至少有一名志愿者.⑴求甲、乙兩人同時參加![]() 崗位服務的概率;⑵求甲、乙兩人不在同一個崗位服務的概率;⑶設隨機變量
崗位服務的概率;⑵求甲、乙兩人不在同一個崗位服務的概率;⑶設隨機變量![]() 為這五名志愿者中參加
為這五名志愿者中參加![]() 崗位服務的人數,求
崗位服務的人數,求![]() 的分布列和數學期望.
的分布列和數學期望.
甲、乙等五名奧運志愿者被隨機地分到![]() 四個不同的崗位服務,每個崗位至少有一名志愿者.
四個不同的崗位服務,每個崗位至少有一名志愿者.
⑴、求甲、乙兩人同時參加![]() 崗位服務的概率;
崗位服務的概率;
⑵、求甲、乙兩人不在同一個崗位服務的概率;
⑶、設隨機變量![]() 為這五名志愿者中參加
為這五名志愿者中參加![]() 崗位服務的人數,求
崗位服務的人數,求![]() 的分布列.
的分布列.
甲、乙等五名奧運志愿者被隨機地分到 四個不同的崗位服務,每個崗位至少有一名志愿者.(Ⅰ)求甲、乙兩人同時參加
四個不同的崗位服務,每個崗位至少有一名志愿者.(Ⅰ)求甲、乙兩人同時參加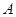 崗位服務的概率;(Ⅱ)求甲、乙兩人不在同一個崗位服務的概率;(Ⅲ)設隨機變量
崗位服務的概率;(Ⅱ)求甲、乙兩人不在同一個崗位服務的概率;(Ⅲ)設隨機變量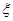 為這五名志愿者中參加
為這五名志愿者中參加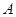 崗位服務的人數,
崗位服務的人數, 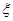 可取何值?請求出相應的
可取何值?請求出相應的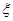 值的分布列.
值的分布列.
甲、乙等五名奧運志愿者被隨機地分到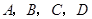 四個不同的崗位服務,每個崗位至少有一名志愿者.(Ⅰ)求甲、乙兩人同時參加
四個不同的崗位服務,每個崗位至少有一名志愿者.(Ⅰ)求甲、乙兩人同時參加 崗位服務的概率;(Ⅱ)求甲、乙兩人不在同一個崗位服務的概率;(Ⅲ)設隨機變量
崗位服務的概率;(Ⅱ)求甲、乙兩人不在同一個崗位服務的概率;(Ⅲ)設隨機變量 為這五名志愿者中參加
為這五名志愿者中參加 崗位服務的人數,
崗位服務的人數,  可取何值?請求出相應的
可取何值?請求出相應的 值的分布列.
值的分布列.
一、選擇題(本大題共8小題,每小題5分,滿分40分.)
題號
1
2
3
4
5
6
7
8
選項
C
A
C
B
D
B
B
A
二、填空題(共7小題,計30分。其中第9、10、11、12小題必做;第13、14、15題選做兩題,若3題全做,按前兩題得分計算。)
9、 4 .10、__10__(用數字作答).11、__.files/image184.gif) __。12、___0___。
__。12、___0___。
13、 .files/image186.gif) ;14、___8_____.15、 3
。
;14、___8_____.15、 3
。
三、解答題(考生若有不同解法,請酌情給分!)
16.解:(1).files/image188.gif) …………2分
…………2分
.files/image190.gif) ……………………………………3分
……………………………………3分
.files/image192.gif)
.files/image194.gif) ………………………………………………5分
………………………………………………5分
(2).files/image196.gif) …………………………7分
…………………………7分
.files/image198.gif)
.files/image200.gif) …………………………………9分
…………………………………9分
.files/image202.gif)
.files/image204.gif) ………………………………………10分
………………………………………10分
故.files/image206.gif)
∴當.files/image208.gif) ………………………………12分
………………………………12分
17.解:⑴、記甲、乙兩人同時參加.files/image138.gif) 崗位服務為事件
崗位服務為事件.files/image211.gif) ,那么
,那么.files/image213.gif) ,即甲、乙兩人同時參加
,即甲、乙兩人同時參加.files/image138.gif) 崗位服務的概率是
崗位服務的概率是.files/image216.gif) .……………………4分
.……………………4分
⑵、記甲、乙兩人同時參加同一崗位服務為事件.files/image218.gif) ,
,
那么.files/image220.gif) ,…………………………………………………………6分
,…………………………………………………………6分
所以,甲、乙兩人不在同一崗位服務的概率是.files/image222.gif) .………8分
.………8分
⑶、隨機變量.files/image140.gif) 可能取的值為1,2.事件“
可能取的值為1,2.事件“.files/image225.gif) ”是指有兩人同時參加
”是指有兩人同時參加.files/image138.gif) 崗位服務,則
崗位服務,則
.files/image228.gif) .所以
.所以.files/image230.gif) ,
,
.files/image140.gif) 的分布列是:…………………………………………………………………… 10分
的分布列是:…………………………………………………………………… 10分
.files/image140.gif)
1
2
.files/image112.gif)
.files/image235.gif)
.files/image237.gif)
∴.files/image239.gif) …………………………………………………………12分
…………………………………………………………12分
18.
解:設2008年末汽車保有量為a1萬輛,以后各年末汽車保有量依次為a2萬輛,a3萬輛,…,每年新增汽車x萬輛。………………………………………………………………1分
a1=30,a2=a1×0.94+x,a3=a2×0.94+x=a1×0.942+x×0.94+x,…
故an=a1×0.94n-1+x(1+0.94+…+0.94n-2)
.files/image241.gif) .………………………………………………6分
.………………………………………………6分
(1):當x=3萬輛時,an.files/image243.gif) ≤30
≤30
則每年新增汽車數量控制在3萬輛時,汽車保有量能達到要求。……………9分
(2):如果要求汽車保有量不超過60萬輛,即an≤60(n=1,2,3,…)
則.files/image245.gif) ,
,
即.files/image247.gif) .
.
對于任意正整數n,.files/image249.gif)
因此,如果要求汽車保有量不超過60萬輛,x≤3.6(萬輛).………………13分
答:若每年新增汽車數量控制在3萬輛時,汽車保有量能達到要求;每年新增汽車不應超過3.6萬輛,則汽車保有量定能達到要求。………………………………………14分
19.解:(1).files/image251.gif) …………………………………………………………2分
…………………………………………………………2分
由己知.files/image253.gif) 有實數解,∴
有實數解,∴.files/image255.gif) ,故
,故.files/image257.gif) …………………5分
…………………5分
(2)由題意.files/image153.gif) 是方程
是方程.files/image259.gif) 的一個根,設另一根為
的一個根,設另一根為.files/image261.gif)
則.files/image263.gif) ,∴
,∴.files/image265.gif) ……………………………………………………7分
……………………………………………………7分
∴.files/image267.gif) ,
,.files/image269.gif)
當.files/image271.gif) 時,
時,.files/image273.gif) ;當
;當.files/image275.gif) 時,
時,.files/image277.gif) ;
;
當.files/image279.gif) 時,
時,.files/image273.gif)
∴當.files/image281.gif) 時,
時,.files/image283.gif) 有極大值
有極大值.files/image285.gif) ,又
,又.files/image287.gif) ,
,.files/image289.gif) ,
,
即當.files/image291.gif) 時,
時,.files/image283.gif) 的量大值為
的量大值為.files/image289.gif) ………………………10分
………………………10分
∵對.files/image293.gif) 時,
時,.files/image295.gif) 恒成立,∴
恒成立,∴.files/image297.gif) ,
,
∴.files/image299.gif) 或
或.files/image301.gif) ………………………………………………………………13分
………………………………………………………………13分
故.files/image159.gif) 的取值范圍是
的取值范圍是.files/image303.gif) ………………………………………14分
………………………………………14分
.files/image305.gif)
20.解:(1)作MP∥AB交BC于點P,NQ∥AB交BE于點Q,連結PQ,依題意可得MP∥NQ,且MP=NQ,即MNQP是平行四邊形,
∴MN=PQ.由已知,CM=BN=a,CB=AB=BE=1,
∴AC=BF=.files/image307.gif) ,
, .files/image309.gif) .
.
即CP=BQ=.files/image311.gif) .
.
∴MN=PQ=.files/image313.gif)
.files/image315.gif) (0<a<
(0<a<.files/image307.gif) ).…………………………………5分
).…………………………………5分
(2)由(Ⅰ),MN=.files/image318.gif) ,所以,當a=
,所以,當a=.files/image320.gif) 時,MN=
時,MN=.files/image320.gif) .
.
即M、N分別移動到AC、BF的中點時,MN的長最小,最小值為.files/image320.gif) .………8分
.………8分
(3)取MN的中點G,連結AG、BG,∵AM=AN,BM=BN,G為MN的中點
∴AG⊥MN,BG⊥MN,∠AGB即為二面角α的平面角,………………………11分
又AG=BG=.files/image322.gif) ,所以,由余弦定理有cosα=
,所以,由余弦定理有cosα=.files/image324.gif) .
.
故所求二面角的余弦值為-.files/image326.gif) .………………………………………………………14分
.………………………………………………………14分
(注:本題也可用空間向量,解答過程略)
21.解:⑴、.files/image328.gif) 對任意的正數
對任意的正數.files/image330.gif) 均有
均有.files/image332.gif) 且
且.files/image334.gif) .
.
又.files/image328.gif)
.files/image337.gif)
.files/image339.gif)
.files/image341.gif) ,…………………………………………………4分
,…………………………………………………4分
又.files/image343.gif) 是定義在
是定義在.files/image345.gif) 上的單增函數,
上的單增函數,.files/image339.gif)
.files/image348.gif) .
.
當.files/image350.gif) 時,
時,.files/image352.gif) ,
,.files/image354.gif) .
..files/image356.gif) ,
,.files/image358.gif) .
.
當.files/image360.gif) 時,
時,.files/image362.gif) ,
,
.files/image364.gif) .
..files/image366.gif) ,
,
.files/image368.gif) 為等差數列,
為等差數列,.files/image370.gif) ,
,.files/image372.gif) . ……………………………6分
. ……………………………6分
⑵、假設.files/image374.gif) 存在滿足條件,即
存在滿足條件,即.files/image376.gif)
對一切.files/image378.gif) 恒成立.
恒成立.
令.files/image380.gif) ,
,
.files/image339.gif)
.files/image383.gif) ,………………………10分
,………………………10分
故.files/image385.gif) ,………………………12分
,………………………12分
.files/image387.gif) ,
,.files/image339.gif)
.files/image390.gif) 單調遞增,
單調遞增,.files/image392.gif) ,
,.files/image394.gif)
.files/image396.gif) .
.
.files/image339.gif)
.files/image399.gif) .……………………………………………………………14分
.……………………………………………………………14分
(考生若有不同解法,請酌情給分!)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com