
題目列表(包括答案和解析)
如圖, 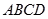 是邊長為
是邊長為 的正方形,
的正方形, 平面
平面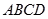 ,
, ,
, ,
, 與平面
與平面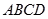 所成角為
所成角為 .
.

(Ⅰ)求證: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)線段 上是否存在點
上是否存在點 ,使得
,使得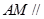 平面
平面 ?若存在,試確定點
?若存在,試確定點 的位置;若不存在,說明理由。
的位置;若不存在,說明理由。
如圖,四棱錐 的底面
的底面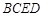 是直角梯形,
是直角梯形, ,
,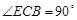 ,
,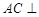 平面
平面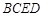 ,
,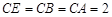 ,
,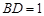 .
.
(1)求直線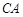 與平面
與平面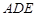 所成角的正弦值;
所成角的正弦值;
(2)在線段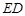 上是否存在一點
上是否存在一點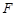 ,使得異面直線
,使得異面直線 與
與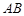 所成角余 弦值等
所成角余 弦值等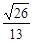 ?若存在,試確定點
?若存在,試確定點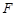 的位置;若不存在,請說明理由.
的位置;若不存在,請說明理由.

如圖,已知三棱柱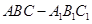 的側棱與底面垂直,
的側棱與底面垂直,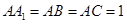 ,
,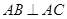 ,
,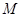 ,
,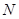 分別是
分別是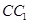 ,
,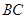 的中點,點
的中點,點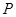 在直線
在直線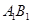 上,且
上,且 ;
;
(Ⅰ)證明:無論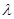 取何值,總有
取何值,總有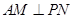 ;
;
(Ⅱ)當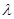 取何值時,直線
取何值時,直線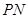 與平面
與平面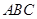 所成的角
所成的角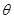 最大?并求該角取最大值時的正切值;
最大?并求該角取最大值時的正切值;
(Ⅲ)是否存在點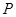 ,使得平面
,使得平面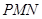 與平面
與平面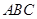 所成的二面角為30º,若存在,試確定點
所成的二面角為30º,若存在,試確定點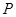 的位置,若不存在,請說明理由.
的位置,若不存在,請說明理由.

如圖,在正三棱柱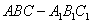 中,已知
中,已知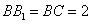 .
.
(1)求直線 所成角的正弦值;
所成角的正弦值;
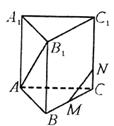 (2)若
(2)若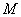 是
是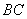 的中點,問在棱
的中點,問在棱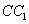 上是否存在點
上是否存在點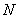 使
使 ,若存在,試確定點
,若存在,試確定點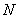 的位置,若不存在,說明理由.
的位置,若不存在,說明理由.
如圖,四棱錐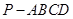 中,底面
中,底面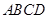 是平行四邊形,
是平行四邊形,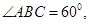
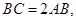
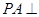 底面
底面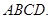
(Ⅰ)求證: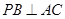 ;(Ⅱ)若
;(Ⅱ)若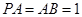 ,求二面角
,求二面角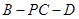 的余弦值;
的余弦值;
(Ⅲ)當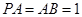 時,在線段
時,在線段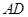 上是否存在一點
上是否存在一點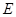 使二面角
使二面角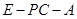 為
為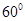 ,若存在,試確定點
,若存在,試確定點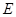 的位置;若不存在,請說明理由。
的位置;若不存在,請說明理由。

一、
|