
題目列表(包括答案和解析)
若函數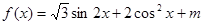 在區間
在區間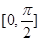 上的最小值為3,
上的最小值為3,
(1)求常數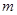 的值;
的值;
(2)求此函數當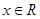 時的最大值和最小值,并求相應的
時的最大值和最小值,并求相應的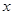 的取值集合。
的取值集合。
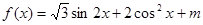 在區間
在區間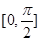 上的最小值為3,
上的最小值為3,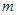 的值;
的值;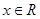 時的最大值和最小值,并求相應的
時的最大值和最小值,并求相應的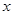 的取值集合。
的取值集合。已知函數 在區間
在區間 ,
, 上單調遞增,在區間[-2,2]上單調遞減.
上單調遞增,在區間[-2,2]上單調遞減.
(1)求 的解析式;
的解析式;
(2)設 ,若對任意的x1、x2
,若對任意的x1、x2 不等式
不等式 恒成立,求實數m的最小值。
恒成立,求實數m的最小值。
已知函數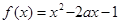 在區間
在區間 上的最大值為
上的最大值為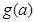 ,最小值為
,最小值為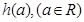 。
。
(1)求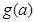 和
和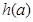 ;
;
(2)作出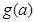 和
和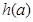 的圖像,并分別指出
的圖像,并分別指出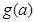 的最小值和
的最小值和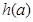 的最大值各為多少?
的最大值各為多少?
已知函數 在區間
在區間 上為增函數,且
上為增函數,且 。
。
(1)當 時,求
時,求 的值;
的值;
(2)當 最小時,
最小時,
①求 的值;
的值;
②若 是
是 圖象上的兩點,且存在實數
圖象上的兩點,且存在實數 使得
使得
 ,證明:
,證明: 。
。
一、選擇題:本大題共有8個小題,每小題5分,共40分;在每個小題給出的四個選項中有且僅有一個是符合題目要求的。
1―8 BDABADBC
二、填空題:本大題共有6個小題,每小題5分,共30分;請把答案寫在相應的位置上。
9.5 10. 11.7 12.
11.7 12. 13.
13. 14.
14.
三、解答題:本大題共6個小題,共80分;解答應寫出文字說明,證明過程或演算步驟。
15.(本題滿分13分)
解:(1)

(2)

16.(本題滿分13分)
解: 用A,B,C分別表示事件甲、乙、丙面試合格.
由題意知A,B,C相互獨立,且
P(A)=P(B)=P(C)= .
.
(Ⅰ)至少有1人面試合格的概率是
 …………………6分
…………………6分
(2)沒有人簽約的概率為

 ………………13分
………………13分
17.(本題滿分13分)
解法1:(1)連結A1B,則D1E在側面ABB
又∵A1B⊥AB1,
|