
題目列表(包括答案和解析)
(A) 3 (B)2 (C)1 (D)-1
設函數f(x)的定義域為D,若存在非零實數l使得對于任意x∈M(M⊆D)有x+l∈D,且f(x+l)≥f(x),則稱f(x)為M上的l高調函數,如果定義域為R的函數f(x)是奇函數,當x≥0時,f(x)=|x-a2|-a2,且f(x)為R上的8高調函數,那么實數a的取值范圍是( )
A. 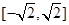 B.
B. 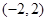 C.
C. 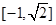 D.
D. 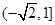
(山東卷理4)設函數f(x)=|x+1|+|x-a|的圖象關于直線x=1對稱,則a的值為
(A) 3 (B)2 (C)1 (D)-1
(山東卷理4)設函數f(x)=|x+1|+|x-a|的圖象關于直線x=1對稱,則a的值為
(A) 3 (B)2 (C)1 (D)-1
 B.
B.  C.
C.  D.
D. 
一.選擇題:本大題共12個小題,每小題5分,共60分.
ABCCB ADCCD BD
二.填空題:本大題共4個小題,每小題5分,共20分.
13. 6 ;14. 60 ;15. ;16 .446.
;16 .446.
三、解答題:本大題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟.
17. (Ⅰ)設 的公比為q(q>0),依題意可得
的公比為q(q>0),依題意可得
 解得
解得 (5分)
(5分)
∴數列 的通項公式為
的通項公式為 (6分)
(6分)
(Ⅱ) (10分)
(10分)
18. (Ⅰ) (2分)∴
(2分)∴ ; (4分)
; (4分)
當 ,即
,即 ,
, 時
時 單調遞增
單調遞增
∴函數 的單調遞增區間為
的單調遞增區間為 (6分)
(6分)
(Ⅱ)∵ ,∴
,∴ ,∴
,∴ (10分)
(10分)
∴當 時,
時, 有最大值
有最大值 ,此時
,此時 .
(12分)
.
(12分)
19.(Ⅰ)記 表示甲以
表示甲以 獲勝;
獲勝; 表示乙以
表示乙以 獲勝,則
獲勝,則 ,
, 互斥,事件
互斥,事件 ,
,
∴
 (6分)
(6分)
 (Ⅱ)
(Ⅱ) 記表示甲以
記表示甲以 獲勝;
獲勝; 表示甲以
表示甲以 獲勝, 則
獲勝, 則 ,
, 互斥,事件
互斥,事件 , ∴
, ∴ (12分)
(12分)
20.
解法一:(Ⅰ)證明:在直三棱柱 中,
中,
面 面ABC,又D為AB中點,∴CD⊥面
面ABC,又D為AB中點,∴CD⊥面 ,∴CD⊥
,∴CD⊥ ,∵AB=
,∵AB= ,∴
,∴ ⊥
⊥ ,
,
又DE∥ ∴
∴ ⊥DE ,又DE∩CD =D
⊥DE ,又DE∩CD =D
∴ ⊥平面CDE (6分)
⊥平面CDE (6分)
(Ⅱ)由(Ⅰ)知 ⊥平面CDE,設
⊥平面CDE,設 與DE交于點M ,
與DE交于點M ,
過B作BN⊥CE,垂足為N,連結MN , 則A1N⊥CE,故∠A1NM即為二面角 的平面角.
(9分)
的平面角.
(9分)
 ∵
∵ ,
, ,又由△ENM △EDC得
,又由△ENM △EDC得
 .
又∵
.
又∵
在Rt△A1MN中,tan∠A1NM  , (12分)
, (12分)
故二面角 的大小為
的大小為 . (12分)
. (12分)
 解法二:AC=BC=2,AB=
解法二:AC=BC=2,AB= ,可得AC⊥BC,故可以C為坐標原點建立如圖所示直角
,可得AC⊥BC,故可以C為坐標原點建立如圖所示直角
坐標系C-xyz.則C(0,0,0),A(2,0,0),B(0,2,0),
D(1,1,0),E (0,2, ),
), (2,0,
(2,0, )(3分)
)(3分)
(Ⅰ) (-2,2,-
(-2,2,- ),
), (1,1,0),
(1,1,0),
 (0,2,
(0,2, ).∵
).∵ ,
,
∴ ,
, 又CE∩CD =C
又CE∩CD =C
∴ ⊥平面CDE
(6分)
⊥平面CDE
(6分)
(Ⅱ)設平面A1CE的一個法向量為n=(x,y,z),  (2,0,
(2,0, ),
),
 (0,2,
(0,2, ).∴由n
).∴由n ,n
,n 得
得 ,
,
令 得
得 ,
, ,n=(2,1,
,n=(2,1, )
(9分)
)
(9分)
又由(Ⅰ)知 (-2,2,-
(-2,2,- )為平面DCE的法向量.
)為平面DCE的法向量.
 等于二面角
等于二面角 的平面角.
(11分)
的平面角.
(11分)
 .
(12分)
.
(12分)
二面角 的大小為
的大小為 .
(12分)
.
(12分)
21.(Ⅰ) .由題意知
.由題意知 為方程
為方程 的兩根
的兩根
由 ,得
,得 (3分)
(3分)
從而 ,
, .
.
當 時,
時, ;當
;當 和
和 時,
時,
故 在
在 上單調遞減,在
上單調遞減,在 ,
, 上單調遞增. (7分)
上單調遞增. (7分)
(Ⅱ)由(Ⅰ)知 在
在 上單調遞減,
上單調遞減, 在
在 處取得極值,此時
處取得極值,此時 ,若存在
,若存在 ,使得
,使得 ,
,
即有 就是
就是 解得
解得 .
(12分)
.
(12分)
故b的取值范圍是 . (12分)
. (12分)
22. (Ⅰ)設橢圓方程為 (a>b>0),由已知c=1,
(a>b>0),由已知c=1,
又2a=  . 所以a=
. 所以a= ,b2=a2-c2=1,
,b2=a2-c2=1,
橢圓C的方程是 + x2
=1. (4分)
+ x2
=1. (4分)
(Ⅱ)若直線l與x軸重合,則以AB為直徑的圓是x2+y2=1,
若直線l垂直于x軸,則以AB為直徑的圓是(x+ )2+y2=
)2+y2= .
.
由 解得
解得 即兩圓相切于點(1,0).
即兩圓相切于點(1,0).
因此所求的點T如果存在,只能是(1,0).
事實上,點T(1,0)就是所求的點.證明如下: (7分)
當直線l垂直于x軸時,以AB為直徑的圓過點T(1,0).
若直線l不垂直于x軸,可設直線l:y=k(x+ ).
).
由 即(k2+2)x2+
即(k2+2)x2+ k2x+
k2x+ k2-2=0.
k2-2=0.
記點A(x1,y1),B(x2,y2),則
又因為 =(x1-1, y1),
=(x1-1, y1),  =(x2-1, y2),
=(x2-1, y2),
 ?
? =(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+
=(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+k2(x1+ )(x2+
)(x2+ )
)
=(k2+1)x1x2+( k2-1)(x1+x2)+
k2-1)(x1+x2)+ k2+1
k2+1
=(k2+1)
 +(
+( k2-1)
k2-1)  +
+
 +1=0, (11分)
+1=0, (11分)
所以TA⊥TB,即以AB為直徑的圓恒過點T(1,0).
所以在坐標平面上存在一個定點T(1,0)滿足條件. (12分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com