
題目列表(包括答案和解析)
 =0與點D有公共點,試求a的最小值。
=0與點D有公共點,試求a的最小值。 已知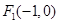 ,
, ,圓
,圓 ,一動圓在
,一動圓在 軸右側(cè)與
軸右側(cè)與 軸相切,同時與圓
軸相切,同時與圓 相外切,此動圓的圓心軌跡為曲線C,曲線E是以
相外切,此動圓的圓心軌跡為曲線C,曲線E是以 ,
, 為焦點的橢圓。
為焦點的橢圓。
(1)求曲線C的方程;
(2)設(shè)曲線C與曲線E相交于第一象限點P,且 ,求曲線E的標(biāo)準(zhǔn)方程;
,求曲線E的標(biāo)準(zhǔn)方程;
(3)在(1)、(2)的條件下,直線 與橢圓E相交于A,B兩點,若AB的中點M在曲線C上,求直線
與橢圓E相交于A,B兩點,若AB的中點M在曲線C上,求直線 的斜率
的斜率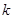 的取值范圍。
的取值范圍。
已知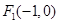 ,
,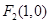 ,圓
,圓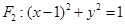 ,一動圓在
,一動圓在 軸右側(cè)與
軸右側(cè)與 軸相切,同時與圓
軸相切,同時與圓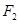 相外切,此動圓的圓心軌跡為曲線C,曲線E是以
相外切,此動圓的圓心軌跡為曲線C,曲線E是以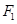 ,
,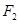 為焦點的橢圓。
為焦點的橢圓。
(1)求曲線C的方程;
(2)設(shè)曲線C與曲線E相交于第一象限點P,且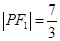 ,求曲線E的標(biāo)準(zhǔn)方程;
,求曲線E的標(biāo)準(zhǔn)方程;
(3)在(1)、(2)的條件下,直線 與橢圓E相交于A,B兩點,若AB的中點M在曲線C上,求直線
與橢圓E相交于A,B兩點,若AB的中點M在曲線C上,求直線 的斜率
的斜率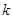 的取值范圍。
的取值范圍。
 (λ>0),
(λ>0), 時,(1)所得曲線記為C,已知直線l:
時,(1)所得曲線記為C,已知直線l: +y=1,P是l上的動點,射線OP(O為坐標(biāo)原點)交曲線C于點R,又點Q在OP上且滿足|OQ|·|OP|=|OR|2,求點Q的軌跡方程。
+y=1,P是l上的動點,射線OP(O為坐標(biāo)原點)交曲線C于點R,又點Q在OP上且滿足|OQ|·|OP|=|OR|2,求點Q的軌跡方程。 
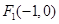 ,
,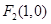 ,圓
,圓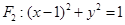 ,一動圓在
,一動圓在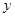 軸右側(cè)與
軸右側(cè)與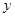 軸相切,同時與圓
軸相切,同時與圓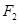 相外切,此動圓的圓心軌跡為曲線C,曲線E是以
相外切,此動圓的圓心軌跡為曲線C,曲線E是以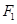 ,
,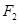 為焦點的橢圓。
為焦點的橢圓。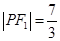 ,求曲線E的標(biāo)準(zhǔn)方程;
,求曲線E的標(biāo)準(zhǔn)方程;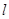 與橢圓E相交于A,B兩點,若AB的中點M在曲線C上,求直線
與橢圓E相交于A,B兩點,若AB的中點M在曲線C上,求直線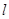 的斜率
的斜率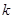 的取值范圍。
的取值范圍。一、選擇題(本大題共12小題,每題5分,共60分)
1.A 2.B 3.C 4.A 5.D 6.C 7.B 8.C 9.A
10.B 11.(理)C(文)B 12.D
二、填空題(本大題共4小題,每題4分,共16分)
13.年度高三測試卷數(shù)學(xué)(2).files/image132.gif) 14.②③ 15.47 16.□
14.②③ 15.47 16.□
三、解答題(本大題共6小題,共計76分)
17.解:(1)依題意函數(shù)年度高三測試卷數(shù)學(xué)(2).files/image110.gif) 的圖象按向量
的圖象按向量年度高三測試卷數(shù)學(xué)(2).files/image134.gif) 平移后得
平移后得
年度高三測試卷數(shù)學(xué)(2).files/image048.gif)
年度高三測試卷數(shù)學(xué)(2).files/image136.gif) ………………………2分
………………………2分
即年度高三測試卷數(shù)學(xué)(2).files/image048.gif) =
=年度高三測試卷數(shù)學(xué)(2).files/image138.gif) ………………………4分
………………………4分
又年度高三測試卷數(shù)學(xué)(2).files/image140.gif)
比較得a=1,b=0 ………………………6分
(2)年度高三測試卷數(shù)學(xué)(2).files/image142.gif)
=年度高三測試卷數(shù)學(xué)(2).files/image144.gif) ………………………9分
………………………9分
年度高三測試卷數(shù)學(xué)(2).files/image146.gif)
年度高三測試卷數(shù)學(xué)(2).files/image148.gif)
∴年度高三測試卷數(shù)學(xué)(2).files/image104.gif) 的單調(diào)增區(qū)間為[
的單調(diào)增區(qū)間為[年度高三測試卷數(shù)學(xué)(2).files/image151.gif) ,
,年度高三測試卷數(shù)學(xué)(2).files/image153.gif) ]
]年度高三測試卷數(shù)學(xué)(2).files/image155.gif) ……………………12分
……………………12分
18.解:
(1)設(shè)連對的個數(shù)為y,得分為x
因為y=0,1,2,4,所以x=0,2,4,8.
年度高三測試卷數(shù)學(xué)(2).files/image157.gif)
|