日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

如圖，拋物線y＝x²－2x－8交y軸于點A，交x軸正半軸于點B．

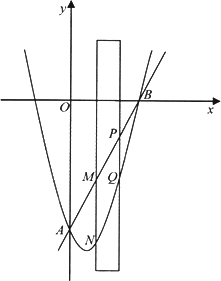
(1)求直線AB對應的函數關系式；

(2)有一寬度為1的直尺平行于y軸，在點A、B之間平行移動，直尺兩長邊所在直線被直線AB和拋物線截得兩線段MN、PQ．設M點的橫坐標為m，且0＜m＜3．試比較線段MN與PQ的大小．

在平面直角坐標系xOy中，已知二次函數y＝x²＋mx＋n的圖象經過點A(2，0)和點B(1，－)，直線l經過拋物線的頂點且與y軸垂直，垂足為Q．

(1)求該二次函數的表達式；

(2)設拋物線上有一動點P從點B處出發沿拋物線向上運動，其縱坐標y₁隨時間t(t≥0)的變化規律為y₁＝－＋2t．現以線段OP為直徑作⊙C．

①當點P在起始位置點B處時，試判斷直線l與⊙C的位置關系，并說明理由；在點P運動的過程中，直線l與⊙C是否始終保持這種位置關系？請說明你的理由；

②若在點P開始運動的同時，直線l也向上平行移動，且垂足Q的縱坐標y₂隨時間t的變化規律為y₂＝－1＋3t，則當t在什么范圍內變化時，直線l與⊙C相交？此時，若直線l被⊙C所截得的弦長為a，試求a²的最大值．

已知拋物線y＝x²＋(2n－1)x＋n²－1(n為常數)．

(1)當該拋物線經過坐標原點，并且頂點在第四象限時，求出它所對應的函數關系式；

(2)設A是(1)所確定的拋物線上位于x軸下方且在對稱軸左側的一個動點，過點A作x軸的平行線，交拋物線于另一點D，再作AB⊥x軸于點B，DC⊥x軸于點C．

①當BC＝1時，求矩形ABCD的周長；

②當矩形ABCD的周長最大時，求出這個最大值，指出此時點A的坐標．

已知拋物線y＝x²＋(2n－1)x＋n²－1(n為常數)．

(1)當該拋物線經過坐標原點，并且頂點在第四象限時，求出它所對應的函數關系式；

(2)設A是(1)所確定的拋物線上位于x軸下方、且在對稱軸左側的一個動點，過A作x軸的平行線，交拋物線于另一點D，再作AB⊥x軸于B，DC⊥x軸于C．

①當BC＝1時，求矩形ABCD的周長；

②試問矩形ABCD的周長是否存在最大值？如果存在，請求出這個最大值，并指出此時A點的坐標；如果不存在，請說明理由．