
題目列表(包括答案和解析)
定義:已知函數f(x)與g(x),若存在一條直線y=kx +b,使得對公共定義域內的任意實數均滿足g(x)≤f(x)≤kx+b恒成立,其中等號在公共點處成立,則稱直線y=kx +b為曲線f(x)與g(x)的“左同旁切線”.已知
(I)證明:直線y=x-l是f(x)與g(x)的“左同旁切線”;
(Ⅱ)設P(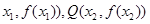 是函數 f(x)圖象上任意兩點,且0<x1<x2,若存在實數x3>0,使得
是函數 f(x)圖象上任意兩點,且0<x1<x2,若存在實數x3>0,使得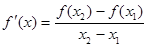 .請結合(I)中的結論證明:
.請結合(I)中的結論證明: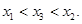
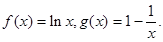
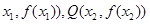 是函數 f(x)圖象上任意兩點,且0<x1<x2,若存在實數x3>0,使得
是函數 f(x)圖象上任意兩點,且0<x1<x2,若存在實數x3>0,使得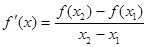 .請結合(I)中的結論證明:
.請結合(I)中的結論證明: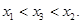
| |||||
| |||||
 與
與 都是非零向量,則“
都是非零向量,則“ ”是“
”是“ ”的充要條件;②已知等腰△ABC的腰為底的2倍,則頂角A的正切值是
”的充要條件;②已知等腰△ABC的腰為底的2倍,則頂角A的正切值是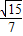 ;③在平面直角坐標系xoy中,四邊形ABCD的邊AB∥DC,AD∥BC,已知點A(-2,0),B(6,8),C(8,6),則D點的坐標為(0,-1);④設
;③在平面直角坐標系xoy中,四邊形ABCD的邊AB∥DC,AD∥BC,已知點A(-2,0),B(6,8),C(8,6),則D點的坐標為(0,-1);④設 ,
, ,
, 為同一平面內具有相同起點的任意三個非零向量,且滿足
為同一平面內具有相同起點的任意三個非零向量,且滿足 與
與 不共線,
不共線, ⊥
⊥ ,|
,| |=|
|=| |,則|
|,則| •
• |的值一定等于以
|的值一定等于以 ,
, 為鄰邊的平行四邊形的面積.其中正確命題的序號是 .(寫出全部正確結論的序號)
為鄰邊的平行四邊形的面積.其中正確命題的序號是 .(寫出全部正確結論的序號)必做部分
1. 2.
2. 3.
3. 4.2.6 5.
4.2.6 5. 6.640+80π 7.
6.640+80π 7. 8.①④ 9.
8.①④ 9. 10.
10.
11.“ ,使得
,使得 且
且 ” 12.
” 12. 13.6 14.9
13.6 14.9
(12.圖13.作 則
則 因
因 ,故
,故 ,
, )
)
15.(1)取AB的中點G,則易證得A1G∥D1F.
又正方形A1ABB1中,E、G分別是相應邊的中點,
∴A1G⊥AE,∴D1F⊥AE.
(2)由正方體可知:A1 D1⊥面A1ABB1,∴A1D1⊥AE .
又由(1)已證:D1F⊥AE.
∵A1D1∩D1F= D1,∴AE⊥平面A1FD1 .
又 平面AED,∴平面AED⊥平面A1FD1 .
平面AED,∴平面AED⊥平面A1FD1 .
16.(1)全班32名學生中,有15名女生,17名男生.在偽代碼中,根據“S←S/15,T←T/17”可以推知,“k=1”和“k=0”分別代表男生和女生;S,T,A分別代表女生、男生及全班成績的平均分;橫線①處應填“(S+T)/32”.
(2)女生、男生及全班成績的平均分分別為S=78,T=76.88,A≈77.4.
(3)15名女生成績的平均分為78,17名男生成績的平均分為77.88.從中可以看出女生成績比較集中,整體水平稍高于男生;男生中的高分段比女生高,低分段比女生多,相比較男生兩極分化比較嚴重.
17.(1)

 .
. ,
, 由題意可知
由題意可知
解得 .
.
(2)由(Ⅰ)可知 的最大值為1,
的最大值為1, .
.
 ,
, . 而
. 而 ,
,
 .
.
由余弦定理知 ,
,
 ,聯立解得
,聯立解得
 .
.
18.(1)設A、B兩點的坐標分別為 得
得 , 根據韋達定理,得
, 根據韋達定理,得
∴線段AB的中點坐標為( ).
).
由已知得
故橢圓的離心率為 .
.
(2)由(1)知 從而橢圓的右焦點坐標為
從而橢圓的右焦點坐標為 設
設 關于直線
關于直線 :
: 的對稱點為
的對稱點為 解得
解得 .由已知得
.由已知得  ,故所求的橢圓方程為
,故所求的橢圓方程為 .
.
19.(1)方法一: .由題設,得
.由題設,得 , ①
, ①
 .
②
.
②
∵ ,∴
,∴ ,∴
,∴ .
.
由①代入②得 ,∴
,∴ ,
,
得 ∴
∴ 或
或 .
③
.
③
將 代入
代入 中,得
中,得 . ④
. ④
由③、④得 ;
;
方法二:∵ ,∴
,∴ ,∴
,∴ .
.
同上可得 將(1)變為
將(1)變為 代入(2)可得
代入(2)可得  ,所以
,所以 ,則
,則 .
.
方法三:同上可得 將(1)變為
將(1)變為 代入(2)可得
代入(2)可得 ,顯然
,顯然 ,所以
,所以 .
.
因為 圖象的開口向下,且有一根為x1=1,
圖象的開口向下,且有一根為x1=1,
由韋達定理得 ,
, .
.
 ,所以
,所以 ,即
,即 ,則
,則 ,
,
由 得
得  ,所以
,所以  .
.
(2)由(1)知, 的判別式Δ=
的判別式Δ=
∴方程 有兩個不等的實根
有兩個不等的實根 ,
,
又 ,∴
,∴ ,
,
∴當 或
或 時,
時, ;當
;當 時,
時, .
.
∴函數 的單調增區間是
的單調增區間是 ,
,  .
.
由 知
知 .
.
∵函數 在區間
在區間 上單調遞增,∴
上單調遞增,∴ ,
,
∴ ,即
,即 的取值范圍是
的取值范圍是 .
.
(3)由 ,即
,即 ,∵
,∵ ,
,

 ,∴
,∴ ,∴
,∴ 或
或 .(自注:視為
.(自注:視為 的一次函數)
的一次函數)
由題意,得 ,∴
,∴ .
.
∴存在實數 滿足條件,即
滿足條件,即 的最小值為
的最小值為 .
.
20.(1)由于 ,則
,則 ,
,
∴ ,∴
,∴ .
.
(2)由于 ,由(1)
,由(1) ,則
,則 ,
, ,
,
而 ,則
,則 ,∴
,∴ ;
;
又 ,
,
∴
 .
.
 ,
,
∴ .
.
而 ,且
,且 ,故
,故 , ∴
, ∴ ,因此
,因此 .
.
從而
選做部分
1. (1)設事件 表示“甲選做14題”,事件
表示“甲選做14題”,事件 表示“乙選做14題”,則甲、乙2名學生選做同一道題的事件為“
表示“乙選做14題”,則甲、乙2名學生選做同一道題的事件為“ ”,且事件
”,且事件 、
、 相互獨立.
相互獨立.
∴  =
= .
.
(2)隨機變量 的可能取值為0,1,2,3,4.且
的可能取值為0,1,2,3,4.且 .
.
∴  .
.
所以變量 的分布列為:
的分布列為:

0
1
2
3
4






 . (或
. (或 )
)
2.以A為原點, 分別為x軸,y軸,z軸的正向建立空間直角坐標系A-xyz,則有
分別為x軸,y軸,z軸的正向建立空間直角坐標系A-xyz,則有
D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2).
于是  ,
, .
.
(1)設EC1與FD1所成角為b,則 .
.
(2)設向量 與平面C1DE垂直,則有
與平面C1DE垂直,則有
 .
.
∴ 其中z>0.
其中z>0.
取n0=(-1,-1,2),則n0是一個與平面C1DE垂直的向量.
∵向量 =(0,0,2)與平面CDE垂直,
=(0,0,2)與平面CDE垂直,
∴n0與 所成的角θ為二面角C-DE-C1的平面角.
所成的角θ為二面角C-DE-C1的平面角.
∵ ,∴
,∴ .
.
3.(1)設M= ,則
,則
 =8
=8 =
= ,故
,故

 =
= ,故
,故
聯立以上兩方程組解得a=6,b=2,c=4,d=4,故M= .
.
(2)由(1)知,矩陣M的特征多項式為 ,故其另一個特征值為
,故其另一個特征值為 .設矩陣M的另一個特征向量是e2
.設矩陣M的另一個特征向量是e2 ,則M e2=
,則M e2= ,解得
,解得 .
.
(3)設點 是直線
是直線 上的任一點,其在矩陣M的變換下對應的點的坐標為
上的任一點,其在矩陣M的變換下對應的點的坐標為 ,則
,則

 =
= ,即
,即 ,
,
代入直線 的方程后并化簡得
的方程后并化簡得 ,即
,即 .
.
4.(1)拋物線焦點為(1,0).
設 :
: 消去x得
消去x得
 ,
,
則 ,
,

= .
.
(2)設 :
: 消去x,得
消去x,得 .
.
 ,則y1+y2=4t ,y1y2=-4b.
,則y1+y2=4t ,y1y2=-4b.

= .
.
令 ,∴直線l過定點(2,0).
,∴直線l過定點(2,0).
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com