日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

(2)是否存在k.t使?若存在.求出k的取值范圍,若不存在.請說明理由. 【查看更多】

 

題目列表(包括答案和解析)

在平面直角坐標系中，已知向量
OF
=(c，0)(c為常數，且c＞0)，
OG
=(x，x)(x∈R)，|
FG
|的最小值為1，
OE
=(
a2
C
，t）（a為常數，且a＞c，t∈R）．動點P同時滿足下列三個條件：
（1）|
PF
|=
c
a
|
PE
|；(2)
PE
=λ•
OF
(λ∈R，且λ≠0)；
（2）動點P的軌跡C經過點B（0，-1）．
（Ⅰ）求曲線C的方程；
（Ⅱ）是否存在方向向量為m=（1，k）（k≠0）的直線l，l與曲線C相交于M、N兩點，使|
BM
|=|
BN
|，且
BM
與
BN
的夾角為60°？若存在，求出k值，并寫出直線l的方程；若不存在，請說明理由．

查看答案和解析>>

對于給定數列{cn}，如果存在實常數p、q，使得cn+1＝pcn＋q對于任意n∈N*都成立，我們稱數列{cn}是“k類數列”．

(Ⅰ)若an＝2n，bn＝3·2n，n∈N*，數列{an}、{bn}是否為“k類數列”？若是，指出它對應的實常數p、q，若不是，請說明理由；

(Ⅱ)證明：若數列{an}是“k類數列”，則數列{an＋an+1}也是“k類數列”；

(Ⅲ)若數列{an}滿足a1＝2，an＋an+1＝3t·2n(n∈N*)，t為常數．求數列{an}前2012項的和．并判斷{an}是否為“k類數列”，說明理由．

查看答案和解析>>

（2006•朝陽區三模）在平面直角坐標系中，已知向量
OF
=（c，0）（c為常數，且c＞0），
OG
=（x，x）（x∈R），
|
FG
|的最小值為  1 ，  
OE
=(
a2
c
，  t)（a為常數，且a＞c，t∈R）．動點P同時滿足下列三個條件：（1）|
PF
|=
c
a
|
PE
|；（2）
PE
=λ
OF
（λ∈R，且λ≠0）；（3）動點P的軌跡C經過點B（0，-1）．
（Ⅰ）求曲線C的方程；
（Ⅱ）是否存在方向向量為
m
=（1，k）（k≠0）的直線l，l與曲線C相交于M、N兩點，使|
BM
|=|
BN
|，且
BM
與
BN
的夾角為60°？若存在，求出k值，并寫出直線l的方程；若不存在，請說明理由．

查看答案和解析>>

已知直線y＝kx＋1(k∈R)與圓C：x2＋y2＝4相交于點A、B，M為弦AB中點

(Ⅰ)當k＝1時，求弦AB的中點M的坐標；

(Ⅱ)當k變化時，是否存在定點T使得MT為定長？若存在，求出定點坐標；若不存在，請說明理由．

查看答案和解析>>

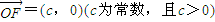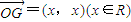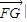在平面直角坐標系中，已知向量，，|的最小值為1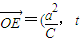，）（a為常數，且a＞c，t∈R）．動點P同時滿足下列三個條件：
（1）•；
（2）動點P的軌跡C經過點B（0，-1）．
（Ⅰ）求曲線C的方程；
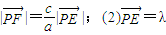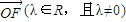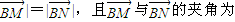（Ⅱ）是否存在方向向量為m=（1，k）（k≠0）的直線l，l與曲線C相交于M、N兩點，使|60°？若存在，求出k值，并寫出直線l的方程；若不存在，請說明理由．

查看答案和解析>>


同步練習冊答案
主站蜘蛛池模板： 91在线中文字幕 | 国产精品无码专区在线观看 | 久久久蜜桃视频 | 亚洲福利国产 | 国产成人av一区二区三区 | 精品国产91亚洲一区二区三区www | 欧美一区黄 | 91污在线 | 亚洲精品在线观 | 日本一区二区精品 | 亚洲国产精品一区二区久久 | 色精品 | 超碰天堂 | 日韩欧美一区二区在线 | 在线观看日韩av | 伊人天天操 | 成人99 | 亚洲一区二区三区在线播放 | 亚洲免费电影一区 | 欧美成人精品一区 | 亚洲午夜精品一区二区三区他趣 | 久久99精品国产自在现线 | 免费三级电影网站 | 亚洲在线观看免费视频 | 成人免费视频网站在线看 | 日韩视频一区 | 99精品欧美一区二区三区 | 国产美女自拍视频 | 久久免费精品视频 | 欧美第7页 | 免费av在线播放 | 国产最新网站 | 国内外成人在线视频 | 色爽| 免费黄色毛片网站 | 色综合天天 | 久久艹精品视频 | 午夜黄色av | 日韩成人精品视频 | 一区二区三区免费av | 91精品在线看 |