
題目列表(包括答案和解析)
| x | 4 |
| 1 |
| 2 |
| 1 |
| S2n-1S2n |
| 8n |
| 3n+4 |
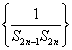 前
前已知點![]() 順次為直線
順次為直線![]() 上的點,點
上的點,點![]() 順次為x軸上的點,其中
順次為x軸上的點,其中![]() 對于任意自然數n,點An,Bn,An+1構成以Bn為頂點的等腰三角形。
對于任意自然數n,點An,Bn,An+1構成以Bn為頂點的等腰三角形。
(1)求數列{yn}的通項公式,并證明它為等差數列;
(2)求證:![]() 是常數,并求數列
是常數,并求數列![]() 的通項公式;
的通項公式;
(3)上述等腰△![]() 中是否可能存在直角三角形,若可能,求出此時a的值;若
中是否可能存在直角三角形,若可能,求出此時a的值;若
不可能,請說明理由。
已知點![]() 順次為直線
順次為直線![]() 上的點,點
上的點,點![]() 順次為x軸上的點,其中
順次為x軸上的點,其中![]() 對于任意自然數n,點An,Bn,An+1構成以Bn為頂點的等腰三角形。
對于任意自然數n,點An,Bn,An+1構成以Bn為頂點的等腰三角形。
(1)求數列{yn}的通項公式,并證明它為等差數列;
(2)求證:![]() 是常數,并求數列
是常數,并求數列![]() 的通項公式;
的通項公式;
(3)上述等腰△![]() 中是否可能存在直角三角形,若可能,求出此時a的值;若
中是否可能存在直角三角形,若可能,求出此時a的值;若
不可能,請說明理由。
1. ; 2. 2. 3.200 4. 3 5.
; 2. 2. 3.200 4. 3 5. 6.
6. 7.
7.
8.6 9. ; 10.
; 10. 11.1005 12.4 13. 1 14.
11.1005 12.4 13. 1 14.
 15.解: (1).如圖,
15.解: (1).如圖, ,
,
即 .
.
(2).在 中,由正弦定理得
中,由正弦定理得

由(1)得 ,
,
即 .
.

16.解:(Ⅰ) 在△PAC中,∵PA=3,AC=4,PC=5,
 ∴
∴ ,∴
,∴ ;又AB=4,PB=5,∴在△PAB中,
;又AB=4,PB=5,∴在△PAB中,
同理可得 
∵ ,∴
,∴
∵ 平面ABC,∴PA⊥BC.
平面ABC,∴PA⊥BC.
(Ⅱ) 如圖所示取PC的中點G,
連結AG,BG,∵PF:FC=3:1,∴F為GC的中點
又D、E分別為BC、AC的中點,
∴AG∥EF,BG∥FD,又AG∩GB=G,EF∩FD=F……………7分
∴面ABG∥面DEF
即PC上的中點G為所求的點 …………… 9分
(Ⅲ)
17.解:(1)由題意得 ,
,
整理得 ,解得
,解得 ,
,
所以“學習曲線”的關系式為 .
.
(2)設從第 個單位時間起的2個單位時間內的平均學習效率為
個單位時間起的2個單位時間內的平均學習效率為 ,則
,則

令 ,則
,則 ,
,
顯然當 ,即
,即 時,
時, 最大,
最大,
將 代入
代入 ,得
,得 ,
,
所以,在從第3個單位時間起的2個單位時間內的平均學習效率最高.
18. 解:(1)由題可得 ,
, ,設
,設
則 ,
, ,……………………2分
,……………………2分
∴ ,∵點
,∵點 在曲線上,則
在曲線上,則 ,∴
,∴ ,從而
,從而 ,得
,得 .則點P的坐標為
.則點P的坐標為 . ……………………5分
. ……………………5分
(2)由題意知,兩直線PA、PB的斜率必存在,設PB的斜率為 ,………6分
,………6分
則BP的直線方程為: .由
.由 得
得
 ,設
,設 ,則
,則 ,
,
 同理可得
同理可得 ,則
,則 ,
, . ………………9分
. ………………9分
所以:AB的斜率 為定值. ………………10分
為定值. ………………10分
(3)設AB的直線方程: .
.
由 ,得
,得 ,
,
由 ,得
,得
P到AB的距離為 ,………………12分
,………………12分
則
 。
。
當且僅當 取等號
取等號
∴三角形PAB面積的最大值為 。………………14分
。………………14分
19.解:
(1)依題意有 ,于是
,于是 .
.
所以數列 是等差數列.
是等差數列.
 .4分
.4分
(2)由題意得 ,即
,即 , (
, ( )
①
)
①
所以又有 .
②
.
②
由② ①得:
①得: , 所以
, 所以 是常數.
是常數.
由 都是等差數列.
都是等差數列.
 ,那么得
,那么得  ,
,
 . (
. (


故
 10分
10分
(3) 當 為奇數時,
為奇數時, ,所以
,所以
當 為偶數時,
為偶數時, 所以
所以
作 軸,垂足為
軸,垂足為 則
則 ,要使等腰三角形
,要使等腰三角形 為正三角形,必須且只須:
為正三角形,必須且只須: .
.
當 為奇數時,有
為奇數時,有 ,即
,即 ①
①
 , 當
, 當 時,.
時,.  不合題意.
不合題意.
當 為偶數時,有
為偶數時,有 ,
, ,同理可求得
,同理可求得  .
.
 ;
; ;當
;當 時,
時, 不合題意.
不合題意.
綜上所述,使等腰三角形 中,有正三角形,
中,有正三角形, 的值為
的值為
 ;
; ;
; ;
;
 16分
16分
20⑴當x≥1時, 只需2+a≥0即a≥-2
只需2+a≥0即a≥-2
⑵作差變形可得:

 =
=

 (*)
(*)
 x1>0,x2>o
x1>0,x2>o 

 從而
從而

∴ln ,又a<0 ∴(*)式≥0
,又a<0 ∴(*)式≥0
即 (當且僅當x1=x2時取“=”號)
(當且僅當x1=x2時取“=”號)
 (3)
(3) 可化為:
可化為:
 x
x ∴lnx≤1≤x,因等號不能同時取到,∴lnx<x,lnx―x<0
∴lnx≤1≤x,因等號不能同時取到,∴lnx<x,lnx―x<0
∴a≥
令
 , x
, x ,
,
 =
=
 x
x ,∴lnx―1―
,∴lnx―1― <0,且1―x≤0
<0,且1―x≤0
從而, ,所以g(x)在x
,所以g(x)在x 上遞增,從而
上遞增,從而 =g(1)= ―
=g(1)= ―
由題設a≥―
即存在x ,不等式f(x)≤(a+3)―
,不等式f(x)≤(a+3)― 能成立且a
能成立且a
21.A解(1)利用△CDO≌△BCM,可證MB=OC= AB
AB
(2)由△PMB∽△BMC,得 ,∴BP=
,∴BP=
B、設M= ,則
,則
 =8
=8 =
= ,故
,故

 =
= ,故
,故
聯立以上兩方程組解得a=6,b=2,c=4,d=4,故M= .
.
 C.求直線
C.求直線 (
( )被曲線
)被曲線 所截的弦長,將方程
所截的弦長,將方程 ,
, 分別化為普通方程:
分別化為普通方程:
 ,
, ………(5分)
………(5分)
 D.解:由柯西不等式可得
D.解:由柯西不等式可得 


22、解析:(1)記“
 ”為事件A, (
”為事件A, (
 )的取值共有10種情況,…………1分
)的取值共有10種情況,…………1分
滿足
 的(
的(
 )的取值有以下4種情況:
)的取值有以下4種情況:
(3,2),(4,2),(5,2),(5,4),
所以 ;
;
(2)隨機變量 的取值為2,3,4,5,
的取值為2,3,4,5, 的分布列是
的分布列是

2
3
4
5
P




…………10分
所以 的期望為
的期望為
23、解:(1)由 得
得
∵在數列 中
中 ,∴
,∴ ,∴
,∴
故數列 中的任意一項都小于1
中的任意一項都小于1
(2)由(1)知 ,那么
,那么 ,
,
由此猜想: (n≥2).下面用數學歸納法證明:
(n≥2).下面用數學歸納法證明:
①當n=2時,顯然成立;
②當n=k時(k≥2,k∈N)時,假設猜想正確,即 ,
,
那么 ,
,
∴當n=k+1時,猜想也正確
綜上所述,對于一切 ,都有
,都有 。
。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com