
題目列表(包括答案和解析)
(12分)給定拋物線![]() 是
是![]() 的焦點,過
的焦點,過![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() 兩點.
兩點.
(Ⅰ)設直線![]() 的斜率為1,求
的斜率為1,求![]() 夾角的余弦值;
夾角的余弦值;
(本小題滿分12分)已知直線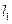
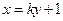 所經過的定點
所經過的定點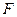 恰好是橢圓
恰好是橢圓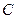 的一個焦點,且橢圓
的一個焦點,且橢圓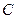 上的點到點
上的點到點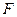 的最大距離為3.
的最大距離為3.
(Ⅰ)求橢圓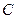 的標準方程;
的標準方程;
(Ⅱ)已知圓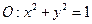 ,直線
,直線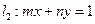 .試證明:當點
.試證明:當點 在橢圓
在橢圓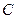 上運動時,直線
上運動時,直線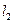 與圓
與圓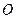 恒相交,并求直線
恒相交,并求直線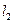 被圓
被圓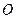 所截得弦長
所截得弦長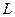 的取值范圍.
的取值范圍.
(Ⅲ)設直線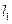 與橢圓交于
與橢圓交于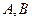 兩點,若直線
兩點,若直線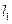 交
交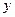 軸于點
軸于點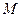 ,且
,且 ,當
,當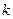 變化時,求
變化時,求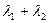 的值;
的值;
(本小題滿分12分)
已知直線![]()
![]() 所經過的定點
所經過的定點![]() 恰好是橢圓
恰好是橢圓![]() 的一個焦點,且橢圓
的一個焦點,且橢圓![]() 上的點到點
上的點到點![]() 的最大距離為3.
的最大距離為3.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)已知圓![]() ,直線
,直線![]() .試證明:當點
.試證明:當點![]() 在橢圓
在橢圓![]() 上運動時,直線
上運動時,直線![]() 與圓
與圓![]() 恒相交,并求直線
恒相交,并求直線![]() 被圓
被圓![]() 所截得弦長
所截得弦長![]() 的取值范圍.
的取值范圍.
(Ⅲ)設直線![]() 與橢圓交于
與橢圓交于![]() 兩點,若直線
兩點,若直線![]() 交
交![]() 軸于點
軸于點![]() ,且
,且![]() ,當
,當![]() 變化時,求
變化時,求![]() 的值;
的值;
(本小題滿分12分)
已知直線![]()
![]() 所經過的定點
所經過的定點![]() 恰好是橢圓
恰好是橢圓![]() 的一個焦點,且橢圓
的一個焦點,且橢圓![]() 上的點到點
上的點到點![]() 的最大距離為3.
的最大距離為3.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)已知圓![]() ,直線
,直線![]() .試證明:當點
.試證明:當點![]() 在橢圓
在橢圓![]() 上運動時,直線
上運動時,直線![]() 與圓
與圓![]() 恒相交,并求直線
恒相交,并求直線![]() 被圓
被圓![]() 所截得弦長
所截得弦長![]() 的取值范圍.
的取值范圍.
(Ⅲ)設直線![]() 與橢圓交于
與橢圓交于![]() 兩點,若直線
兩點,若直線![]() 交
交![]() 軸于點
軸于點![]() ,且
,且![]() ,當
,當![]() 變化時,求
變化時,求![]() 的值;
的值;
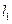
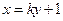 所經過的定點
所經過的定點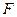 恰好是橢圓
恰好是橢圓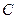 的一個焦點,且橢圓
的一個焦點,且橢圓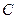 上的點到點
上的點到點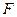 的最大距離為3.
的最大距離為3.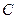 的標準方程;
的標準方程;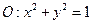 ,直線
,直線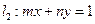 .試證明:當點
.試證明:當點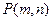 在橢圓
在橢圓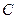 上運動時,直線
上運動時,直線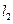 與圓
與圓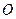 恒相交,并求直線
恒相交,并求直線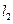 被圓
被圓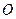 所截得弦長
所截得弦長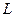 的取值范圍.
的取值范圍.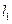 與橢圓交于
與橢圓交于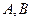 兩點,若直線
兩點,若直線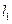 交
交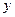 軸于點
軸于點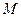 ,且
,且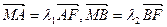 ,當
,當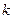 變化時,求
變化時,求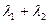 的值;
的值; 一.選擇題
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
B
C
A
D
C
B
A
D
D
A
二.13. 14.
14. 15.
15. 16.
16. (萬元)
(萬元)
三.17.(I) 由
代入
 得:
得:
整理得: (5分)
(5分)
(II)由
 由余弦定理得:
由余弦定理得:
∴
 -----------------------------
(9分)
-----------------------------
(9分)


又
 ------ (12分)
------ (12分)
18.(Ⅰ)  的分布列.
的分布列.

2
3
4
5
6
p





- --------- ------ (4分)
(Ⅱ)設擲出的兩枚骰子的點數同是 為事件
為事件
同擲出1的概率 ,同擲出2的概率
,同擲出2的概率 ,同擲出3的概率
,同擲出3的概率
所以,擲出的兩枚骰子的點數相同的概率為P=

 (8分)
(8分)
(Ⅲ)

 時)
時)

2
3
4
5
6

3
6
6
6
6
p





 =
=
 時)
時)

2
3
4
5
6

2
5
8
8
8
p





 =
=
 時)
時)

2
3
4
5
6

1
4
7
10
10
p





 =
=
 時,
時,  最大為
最大為 (12分)
(12分)
19.(Ⅰ)


 兩兩相互垂直, 連結
兩兩相互垂直, 連結 并延長交
并延長交 于F.
于F.


同理可得



 ------------ (6分)
------------ (6分)
(Ⅱ) 是
是 的重心
的重心
F是SB的中點


梯形的高
 --- (12分)
--- (12分)
【注】可以用空間向量的方法
20.設2,f (a1),
f (a2),
f (a3),
…,f (an), 2n+4的公差為d,則2n+4=2+(n+2-1)d  d=2,
d=2,

 ……………………(4分)
……………………(4分)
(2) ,
,


 --------------------
(8分)
--------------------
(8分)



21.(Ⅰ)∵直線 的斜率為1,拋物線
的斜率為1,拋物線 的焦點
的焦點
∴直線 的方程為
的方程為
由
設
則
又


故  夾角的余弦值為
夾角的余弦值為 ----------------- (6分)
----------------- (6分)
(Ⅱ)由
即得:
由 
從而得直線 的方程為
的方程為
∴ 在
在 軸上截距為
軸上截距為 或
或
∵ 是
是 的減函數
的減函數
∴  從而得
從而得
故 在
在 軸上截距的范圍是
軸上截距的范圍是
 ------------ (12分)
------------ (12分)
22.(Ⅰ) 
 在直線
在直線 上,
上,
?????????????? (4分)
(Ⅱ)
 在
在 上是增函數,
上是增函數, 在
在 上恒成立
上恒成立
所以得  ??????????????? (8分)
??????????????? (8分)
(Ⅲ) 的定義域是
的定義域是 ,
,
①當 時,
時, 在
在 上單增,且
上單增,且 ,
, 無解;
無解;
②當 時,
時, 在
在 上是增函數,且
上是增函數,且 ,
,
 有唯一解;
有唯一解;
③當 時,
時,
那么在 上
上 單減,在
單減,在 上
上 單增,
單增,
而
 時,
時, 無解;
無解;
 時,
時, 有唯一解
有唯一解  ;
;
 時,
時,
那么在 上,
上, 有唯一解
有唯一解
而在 上,設
上,設


即得在 上,
上, 有唯一解.
有唯一解.
綜合①②③得: 時,
時, 有唯一解;
有唯一解;

 時,
時, 無解;
無解;
 時,
時, 有且只有二解.
有且只有二解.
?????????????? (14分)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com